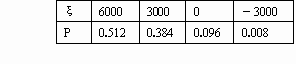Question

解答题

若一台挖掘机每天发生故障的概率均为0.2，发生故障则该天停止工作，该天将亏损1000元，若无故障则该天将获利2000元

(文)分别求出5天内获利4000元和亏损2000元的概率

(理)(1)设3天内所获利润为随机变量ξ，求ξ的分布列；

(理)(2)若每月按30天计算，每月所获利润的平均数为多少？

(理)(3)若请专人维护，每天发生故障的概率可降低到0.1，则每月(按30天计算)最多可给维护人员多少工资？

Answer 1

答案：
解析：

(文)解：由题意，5天内获利4000元，则在5天内有3天无故障，2天发生故障，而每天发生故障是相互独立的，因而其概率 　　P1＝×0.22×(1－0.2)3＝10×0.04×0.512＝0.2048　　　6分 　　5天内亏损2000元，则在5天内有1天无故障，4天发生故障，而每天发生故障是相互独立的，因而其概率为 　　P2＝×0.22×(1－0.2)＝5×0.0016×0.8＝0.0064　　　6分 　　(理)(1)由题意，ξ＝6000、3000、0、－3000，而 　　P(ξ＝6000)＝×0.83＝0.512 　　P(ξ＝3000)＝×0.2×0.82＝0.384 　　P(ξ＝0)＝×0.22×0.8＝0.096 　　P(ξ＝－3000)＝×0.23＝0.008　　　　4分 　　　6分 　　(2)解：由题意，每天利润的平均数为2000×0.8－1000×0.2＝1400(元)， 每天发生的概率是相互独立的， 　　因而，30天的利润为30×1400＝42000(元)　　　9分 　　(3)解：由题意，每月因故障亏损的平均数为30×1000×0.2＝6000(元)， 每月因有维护人员而降低了30×1000×0.1＝3000(元)， 　　因而最多可给工资3000元．　　　12分