题目内容
一种计算装置,有一数据入口点A和一个运算出口点B,按照某种运算程序:①当从A口输入自然数1时,从B口得到
| 1 |
| 3 |
| 1 |
| 3 |
②当从A口输入自然数n(n≥2)时,在B口得到的结果f(n)是前一个结果f(n-1)的
| 2(n-1)-1 |
| 2(n-1)+3 |
试问:当从A口分别输入自然数2,3,4 时,从B口分别得到什么数?试猜想f(n)的关系式,并证明你的结论.
分析:由已知可得,该程序的功能是计算并输出满足条件:①a1=
②an=an-1
的数列第n项an的值.模拟程序的运行过程,依次计算出数列的各项不难给出答案.
| 1 |
| 3 |
| 2(n-1)-1 |
| 2(n-1)+3 |
解答:解:由已知得f(n)=
f(n-1)(n≥2,n∈N*)
当n=2时,f(2)=
×f(1)=
×
=
,
同理可得f(3)=
,f(4)=
---------------------(4分)
猜想f(n)=
-------------------(6分)
下面用数学归纳法证明(*)成立
①当n=1,2,3,4时,由上面的计算结果知(*)成立------(8分)
②假设n=k(k≥4,k∈N*)时,(*)成立,即f(k)=
,
那么当n=k+1时,f(k+1)=
f(k)=
•
即f(k+1)=
∴当n=k+1时,(*)也成立---------------(13分)
综合①②所述,对?n∈N*,f(n)=
成立.-----(14分)
| 2n-3 |
| 2n+1 |
当n=2时,f(2)=
| 4-3 |
| 4+1 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 15 |
同理可得f(3)=
| 1 |
| 35 |
| 1 |
| 63 |
猜想f(n)=
| 1 |
| (2n-1)(2n+1) |
|
下面用数学归纳法证明(*)成立
①当n=1,2,3,4时,由上面的计算结果知(*)成立------(8分)
②假设n=k(k≥4,k∈N*)时,(*)成立,即f(k)=
| 1 |
| (2k-1)(2k+1) |
那么当n=k+1时,f(k+1)=
| 2k-1 |
| 2k+3 |
| 2k-1 |
| 2k+3 |
| 1 |
| (2k-1)(2k+1) |
即f(k+1)=
| 1 |
| [2(k+1)-1][2(k+1)+1] |
综合①②所述,对?n∈N*,f(n)=
| 1 |
| (2n-1)(2n+1) |
点评:算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误.

练习册系列答案
相关题目
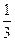 ,记为
,记为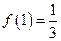 ;②当从A口输入自然数
;②当从A口输入自然数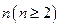 时,在B口得到的结果
时,在B口得到的结果 是前一个结果
是前一个结果 的
的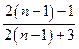 倍.
倍.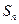 为数列
为数列 的前
的前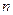 项的和。当从B口得到399的倒数时,求此时对应的
项的和。当从B口得到399的倒数时,求此时对应的 ,记为
,记为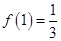 ;
;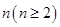 时,在B口得到的结果
时,在B口得到的结果 是前一个结果
是前一个结果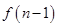 的
的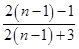 倍;
倍; ,记为
,记为 ;②当从A口输入自然数
;②当从A口输入自然数 时,在B口得到的结果
时,在B口得到的结果 是前一个结果
是前一个结果 的
的 倍.
倍. 为数列
为数列 的前
的前 项的和。当从B口得到399的倒数时,求此时对应的
项的和。当从B口得到399的倒数时,求此时对应的