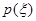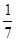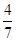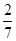题目内容
为了解某校高一年级女生的身高情况,选取一个容量为80的样本(80名女生的身高,单位:cm),分组情况如下:| 分组 | 151.5~158.5 | 158.5~165.5 | 165.5~172.5 | 172.5~179.5 |
| 频数 | 12 | 24 | m | |
| 频率 | a | 0.15 |
(Ⅱ) 试估计身高高于162.0cm的女生的比例.

分析:(I)据频率等于频数除以样本容量,列出方程求m;据频率和为1列出方程求出a.
(II)求出162到165.5的长度乘以此矩形的频率加上其他两个矩形的频率即得高于162.0cm的女生的比例.
(II)求出162到165.5的长度乘以此矩形的频率加上其他两个矩形的频率即得高于162.0cm的女生的比例.
解答: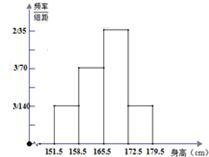 解:(I)
解:(I)
=0.15解得m=12
+
+a+0.15=1解得a=0.4
(Ⅱ)由频率分布直方图,知身高高于162cm同学的比例为[
×
+0.4+0.15]×100%=70%
 解:(I)
解:(I)| m |
| 80 |
| 12 |
| 80 |
| 24 |
| 80 |
(Ⅱ)由频率分布直方图,知身高高于162cm同学的比例为[
| (165.5-162.0) |
| 7 |
| 24 |
| 80 |
点评:在解决频率分布直方图的问题时,一定要注意频率分布直方图的纵坐标是频率除以组距.

练习册系列答案
相关题目
某校为了解高一年级学生身高情况,按10%的比例对全校700名高一学生按性别进行抽样检查,测得身高频数分布表如下:
表1:男生身高频数分布表
|
身高(cm) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
[180,185) |
[185,190) |
|
频数 |
2 |
5 |
13 |
13 |
5 |
2 |
表2:女生身高频数分布表
|
身高(cm) |
[150,155) |
[155,160) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
|
频数 |
1 |
8 |
12 |
5 |
3 |
1 |
(Ⅰ)求该校高一男生的人数;
(Ⅱ)估计该校高一学生身高(单位:cm)在[165,180)的概率;
(Ⅲ)在男生样本中,从身高(单位:cm)在[180,190)的男生中任选3人,设ξ表示所选3人中身高(单位:cm)在[180,185)的人数,求ξ的分布列和数学期望.
|
ξ |
1 |
2 |
3 |
|
|
|
|
|