题目内容
（2009广东卷理）（本小题满分14分）
如图6，已知正方体
的棱长为2，点
是正方形
的中心，点
、
分别是棱
的中点．设点
分别是点，在平面
内的正投影．
（1）求以为顶点，以四边形
在平面内的正投影为底面边界的棱锥的体积；
（2）证明：直线
平面
；
（3）求异面直线
所成角的正弦值.
解析：（1）依题作点
、
在平面
内的正投影
、
，则、分别为
、
的中点，连结
、
、
、
，则所求为四棱锥
的体积，其底面
面积为
，
又
面，
，∴
.
（2）以
为坐标原点，
、
、所在直线分别作
轴，
轴，
轴，得
、
，又
，
，
，则
，
，
，
∴
，
，即
，
，
又
，∴
平面
.
（3）
，
，则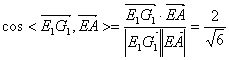
，设异面直线
所成角为
，则
.
练习册系列答案
阅读快车系列答案
相关题目
，集合
和
的关系的韦恩（Venn）图如图1所示，则阴影部分所示的集合的元素共有
与直线
交于两点
和
，且
．记曲线
在点
和点
之间那一段
与线段
所围成的平面区域（含边界）为
．设点
是
与点
是线段
的中点
的轨迹方程； 
与
的最小值．
的中心在坐标原点，长轴在
轴上，离心率为
，且
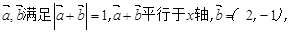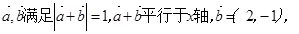则
=
。
则
=
。