题目内容
(理)设l为平面上过点(0,1)的直线,l的斜率等可能地取1,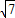 ,-1,-
,-1,-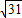 ,用ξ表示坐标原点到l的距离,则随机变ξ的数学期望Eξ= .
,用ξ表示坐标原点到l的距离,则随机变ξ的数学期望Eξ= .
【答案】分析:从4个数字中随机的取一个数字有4种结果,当给定直线的斜率时,写出直线的方程,作出原点到直线的距离,得到变量有三个值,概率比较直接,写出期望值.
解答:解:从4个数字中随机的取一个数字有5种结果,
当直线的斜率为1时,直线的方程是:x-y+1=0
原点到直线的距离是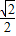 ,
,
当直线斜率是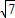 时,直线的方程是
时,直线的方程是 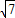 x-y+1=0,
x-y+1=0,
原点到直线的距离是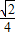 ,
,
当斜率是-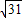 时,直线的方程是
时,直线的方程是 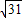 x+y-1=0,
x+y-1=0,
原点到直线的距离是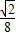 ,
,
∴p(ξ=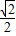 )=
)= ,p(ξ=
,p(ξ=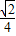 )=
)= ,p(ξ=
,p(ξ=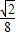 )=
)= ,
,
∴期望值是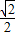 ×
× +
+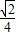 ×
× +
+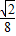 ×
× =
=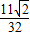
故答案为: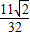
点评:本题考查离散型随机变量的期望和点到直线的距离,是一个综合题目,解题的关键是,写出四条直线的方程,求出距离.
解答:解:从4个数字中随机的取一个数字有5种结果,
当直线的斜率为1时,直线的方程是:x-y+1=0
原点到直线的距离是
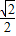 ,
,当直线斜率是
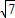 时,直线的方程是
时,直线的方程是 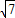 x-y+1=0,
x-y+1=0,原点到直线的距离是
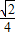 ,
,当斜率是-
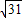 时,直线的方程是
时,直线的方程是 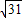 x+y-1=0,
x+y-1=0,原点到直线的距离是
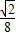 ,
,∴p(ξ=
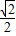 )=
)= ,p(ξ=
,p(ξ=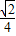 )=
)= ,p(ξ=
,p(ξ=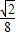 )=
)= ,
,∴期望值是
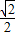 ×
× +
+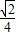 ×
× +
+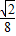 ×
× =
=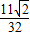
故答案为:
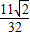
点评:本题考查离散型随机变量的期望和点到直线的距离,是一个综合题目,解题的关键是,写出四条直线的方程,求出距离.

练习册系列答案
相关题目