题目内容
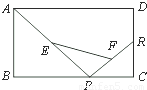
 已知矩形ABCD,R、P分别在边CD、BC上,E、F分别为AP、PR的中点,当P在BC上由B向C运动时,点R在CD上固定不变,设BP=x,EF=y,那么下列结论中正确的是
已知矩形ABCD,R、P分别在边CD、BC上,E、F分别为AP、PR的中点,当P在BC上由B向C运动时,点R在CD上固定不变,设BP=x,EF=y,那么下列结论中正确的是
- A.y是x的增函数
- B.y是x的减函数
- C.y随x先增大后减小
- D.无论x怎样变化,y是常数
D
分析:由已知中R、P分别在边CD、BC上,E、F分别为AP、PR的中点,当P在BC上由B向C运动时,点R在CD上固定不变,我们易根据三角形的中位定理,判断出y为定值,进而比照四个答案,即可得到结论.
解答:连接AR,如图所示:
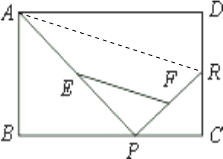
由于点R在CD上固定不变,故AR的长为定值
又∵E、F分别为AP、PR的中点,
∴EF为△APR的中位线,则EF= AR为定值
AR为定值
故无论x怎样变化,y是常数
故选D
点评:本题考查的知识点是函数模型的选择与应用,函数单调性的判断与证明,三角形的中位线定理,其中根据三角形中位定理得到y为定值,是解答本题的关键.
分析:由已知中R、P分别在边CD、BC上,E、F分别为AP、PR的中点,当P在BC上由B向C运动时,点R在CD上固定不变,我们易根据三角形的中位定理,判断出y为定值,进而比照四个答案,即可得到结论.
解答:连接AR,如图所示:

由于点R在CD上固定不变,故AR的长为定值
又∵E、F分别为AP、PR的中点,
∴EF为△APR的中位线,则EF=
 AR为定值
AR为定值故无论x怎样变化,y是常数
故选D
点评:本题考查的知识点是函数模型的选择与应用,函数单调性的判断与证明,三角形的中位线定理,其中根据三角形中位定理得到y为定值,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
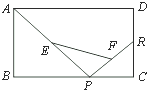
 已知矩形ABCD,R、P分别在边CD、BC上,E、F分别为AP、PR的中点,当P在BC上由B向C运动时,点R在CD上固定不变,设BP=x,EF=y,那么下列结论中正确的是( )
已知矩形ABCD,R、P分别在边CD、BC上,E、F分别为AP、PR的中点,当P在BC上由B向C运动时,点R在CD上固定不变,设BP=x,EF=y,那么下列结论中正确的是( )| A、y是x的增函数 | B、y是x的减函数 | C、y随x先增大后减小 | D、无论x怎样变化,y是常数 |