题目内容
下列6个命题中
(1)第一象限角是锐角
(2)角a终边经过点(a,a)时,sina+cosa=
(3)若y=
sin(ωx)的最小正周期为4π,则ω=
(4)若cos(α+β)=-1,则sin(2α+β)+sinβ=0
(5)若
∥
,则有且只有一个实数λ,使
=λ
.
(6)若定义在R上函数f(x)满足f(x+1)=-f(x),则y=f(x)是周期函数
请写出正确命题的序号______.
(1)第一象限角是锐角
(2)角a终边经过点(a,a)时,sina+cosa=
| 2 |
(3)若y=
| 1 |
| 2 |
| 1 |
| 2 |
(4)若cos(α+β)=-1,则sin(2α+β)+sinβ=0
(5)若
| a |
| b |
| b |
| a |
(6)若定义在R上函数f(x)满足f(x+1)=-f(x),则y=f(x)是周期函数
请写出正确命题的序号______.
361°是第一象限角,但不是锐角,故(1)第一象限角是锐角错误;
∵角a终边经过点(a,a)时,当a=-1时,sina+cosa=-
,故(2)角a终边经过点(a,a)时,sina+cosa=
错误;
若y=
sin(ωx)的最小正周期为4π,则ω=±
,故(3)若y=
sin(ωx)的最小正周期为4π,则ω=
错误;
若cos(α+β)=-1,则sin(α+β)=0,则sin(2α+β)+sinβ=sin[(α+β)+α]+sin[(α+β)-α]=2sin(α+β)cos(α+β)=0,故(4)正确;
若
∥
,则有且只有一个实数λ,使
=λ
.当
=
时不成立,故(5)错误;
若定义在R上函数f(x)满足f(x+1)=-f(x),则y=f(x)是周期为2的周期函数,故(6)正确;
故答案为:(4)、(6)
∵角a终边经过点(a,a)时,当a=-1时,sina+cosa=-
| 2 |
| 2 |
若y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
若cos(α+β)=-1,则sin(α+β)=0,则sin(2α+β)+sinβ=sin[(α+β)+α]+sin[(α+β)-α]=2sin(α+β)cos(α+β)=0,故(4)正确;
若
| a |
| b |
| b |
| a |
| a |
| 0 |
若定义在R上函数f(x)满足f(x+1)=-f(x),则y=f(x)是周期为2的周期函数,故(6)正确;
故答案为:(4)、(6)

练习册系列答案
相关题目

 sin(ωx)的最小正周期为4π,则ω=
sin(ωx)的最小正周期为4π,则ω= ∥
∥ ,则有且只有一个实数λ,使
,则有且只有一个实数λ,使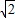
 sin(ωx)的最小正周期为4π,则ω=
sin(ωx)的最小正周期为4π,则ω=
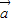 ∥
∥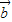 ,则有且只有一个实数λ,使
,则有且只有一个实数λ,使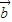 =λ
=λ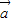 .
.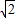
 sin(ωx)的最小正周期为4π,则ω=
sin(ωx)的最小正周期为4π,则ω=
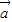 ∥
∥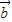 ,则有且只有一个实数λ,使
,则有且只有一个实数λ,使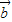 =λ
=λ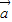 .
.