题目内容
已知双曲线 -
- =1(a>0,b>0)的离心率e=
=1(a>0,b>0)的离心率e= ,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是
,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是 .
.
(1)求双曲线的方程;
(2)过点B作直线m交双曲线于M、N两点,若 •
• =-23,求直线m的方程.
=-23,求直线m的方程.
解:(1)依题意,l方程 +
+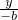 =1,即bx-ay-ab=0,由原点O到l的距离为
=1,即bx-ay-ab=0,由原点O到l的距离为 ,得
,得
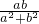 =
= =
= ,又e=
,又e= =
= ,
,
∴b=1,a= .
.
故所求双曲线方程为 -y2=1.
-y2=1.
(2)显然直线m不与x轴垂直,设m方程为y=kx-1,
则点M、N坐标(x1,y1),(x2,y2)是方程组 的解,
的解,
消去y,得(1-3k2)x2+6kx-6=0.①
依题意,1-3k2≠0,由根与系数关系,
知x1+x2=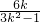 ,x1x2=
,x1x2=
 •
• =(x1,y1)•(x2,y2)=x1x2+y1y2
=(x1,y1)•(x2,y2)=x1x2+y1y2
=x1x2+(kx1-1)(kx2-1)
=(1+k2)x1x2-k(x1+x2)+1
=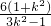 -
-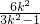 +1=
+1= +1.
+1.
又∵ •
• =-23,
=-23,
∴ +1=-23,k=±
+1=-23,k=± ,
,
当k=± 时,方程①有两个不相等的实数根,
时,方程①有两个不相等的实数根,
∴方程为y= x-1或y=-
x-1或y=- x-1.
x-1.
分析:(1)先求出直线l的方程,再点到直线的距离公式建立关于a,b,c的方程,解这个方程求出a,b,从而得到双曲线的方程.
(2)设m方程为y=kx-1,则点M、N坐标(x1,y1),(x2,y2)是方程组 的解,消去y,得(1-3k2)x2+6kx-6=0.由根与系数关系和题设条件推导出k的值,从而求出直线m的方程.
的解,消去y,得(1-3k2)x2+6kx-6=0.由根与系数关系和题设条件推导出k的值,从而求出直线m的方程.
点评:本题是双典线的综合题,重点考查双曲线的性质及其应用,具有一定的难度.解题时要注意根与系数的关系的灵活运用.
 +
+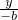 =1,即bx-ay-ab=0,由原点O到l的距离为
=1,即bx-ay-ab=0,由原点O到l的距离为 ,得
,得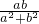 =
= =
= ,又e=
,又e= =
= ,
,∴b=1,a=
 .
.故所求双曲线方程为
 -y2=1.
-y2=1.(2)显然直线m不与x轴垂直,设m方程为y=kx-1,
则点M、N坐标(x1,y1),(x2,y2)是方程组
 的解,
的解,消去y,得(1-3k2)x2+6kx-6=0.①
依题意,1-3k2≠0,由根与系数关系,
知x1+x2=
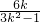 ,x1x2=
,x1x2=
 •
• =(x1,y1)•(x2,y2)=x1x2+y1y2
=(x1,y1)•(x2,y2)=x1x2+y1y2=x1x2+(kx1-1)(kx2-1)
=(1+k2)x1x2-k(x1+x2)+1
=
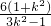 -
-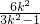 +1=
+1= +1.
+1.又∵
 •
• =-23,
=-23,∴
 +1=-23,k=±
+1=-23,k=± ,
,当k=±
 时,方程①有两个不相等的实数根,
时,方程①有两个不相等的实数根,∴方程为y=
 x-1或y=-
x-1或y=- x-1.
x-1.分析:(1)先求出直线l的方程,再点到直线的距离公式建立关于a,b,c的方程,解这个方程求出a,b,从而得到双曲线的方程.
(2)设m方程为y=kx-1,则点M、N坐标(x1,y1),(x2,y2)是方程组
 的解,消去y,得(1-3k2)x2+6kx-6=0.由根与系数关系和题设条件推导出k的值,从而求出直线m的方程.
的解,消去y,得(1-3k2)x2+6kx-6=0.由根与系数关系和题设条件推导出k的值,从而求出直线m的方程.点评:本题是双典线的综合题,重点考查双曲线的性质及其应用,具有一定的难度.解题时要注意根与系数的关系的灵活运用.

练习册系列答案
相关题目
 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为
,右准线方程为 .
. =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为
,右准线方程为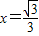 .
. =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为
,右准线方程为 .
. =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为
,右准线方程为 .
.