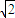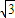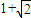题目内容
已知点F是双曲线 的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是直角三角形,则该双曲线的离心率e为
的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是直角三角形,则该双曲线的离心率e为
- A.

- B.2
- C.

- D.

B
分析:利用双曲线的对称性及直角三角形,可得∠AEF=45°,从而|AF|=|EF|,求出|AF|,|EF|得到关于a,b,c的等式,即可求出离心率的值.
解答:∵△ABE是直角三角形,∴∠AEB为直角
∵双曲线关于x轴对称,且直线AB垂直x轴
∴∠AEF=∠BEF=45°
∴|AF|=|EF|
∵F为左焦点,设其坐标为(-c,0)
∴|AF|=
∴|EF|=a+c
∴ =a+c
=a+c
∴c2-ac-2a2=0
∴e2-e-2=0
∵e>1,
∴e=2
故选B.
点评:本题考查双曲线的对称性、考查双曲线的三参数关系:c2=a2+b2、考查双曲线的离心率,属于中档题.
分析:利用双曲线的对称性及直角三角形,可得∠AEF=45°,从而|AF|=|EF|,求出|AF|,|EF|得到关于a,b,c的等式,即可求出离心率的值.
解答:∵△ABE是直角三角形,∴∠AEB为直角
∵双曲线关于x轴对称,且直线AB垂直x轴
∴∠AEF=∠BEF=45°
∴|AF|=|EF|
∵F为左焦点,设其坐标为(-c,0)
∴|AF|=

∴|EF|=a+c
∴
 =a+c
=a+c∴c2-ac-2a2=0
∴e2-e-2=0
∵e>1,
∴e=2
故选B.
点评:本题考查双曲线的对称性、考查双曲线的三参数关系:c2=a2+b2、考查双曲线的离心率,属于中档题.

练习册系列答案
相关题目
 的左焦点,点E是该双曲线的右顶点,过点F且垂直x轴的直线与双曲线交于A,B两点,△
的左焦点,点E是该双曲线的右顶点,过点F且垂直x轴的直线与双曲线交于A,B两点,△ 是直角三角形,则该双曲线的离心率是(
)
是直角三角形,则该双曲线的离心率是(
) B.
B.
 C.
3
D. 2
C.
3
D. 2 的左焦点,点E是该双曲线的右顶点,过点F且垂直x轴的直线与双曲线交于A,B两点,△
的左焦点,点E是该双曲线的右顶点,过点F且垂直x轴的直线与双曲线交于A,B两点,△ 是直角三角形,则该双曲线的离心率是(
)
是直角三角形,则该双曲线的离心率是(
) B.
B.
 C.
2
D. 3
C.
2
D. 3 的左焦点,点E是该双曲线的右顶点,过点F且垂直x轴的直线与双曲线交于A,B两点,△
的左焦点,点E是该双曲线的右顶点,过点F且垂直x轴的直线与双曲线交于A,B两点,△ 是直角三角形,则该双曲线的离心率是(
)
是直角三角形,则该双曲线的离心率是(
) B.
B.
 C.
3
D. 2
C.
3
D. 2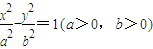 的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是直角三角形,则该双曲线的离心率e为( )
的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是直角三角形,则该双曲线的离心率e为( )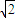
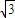
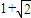
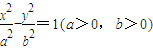 的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是直角三角形,则该双曲线的离心率e为( )
的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是直角三角形,则该双曲线的离心率e为( )