题目内容
设函数![]() ,其中
,其中![]()
(1)求![]() 的取值范围,使得函数
的取值范围,使得函数![]() 在
在![]() 上是单调递减函数;
上是单调递减函数;
(2)此单调性能否扩展到整个定义域![]() 上?
上?
(3)求解不等式![]()
(1)只需要![]() ,就能使
,就能使![]() 在
在![]() 上是单调递减函数;
上是单调递减函数;
(2)此单调性不能扩展到整个定义域上(3)所求解集为![]()
解析:
(1)设![]() ,
,
则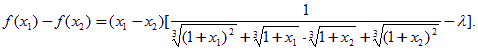
设![]() ,则显然
,则显然![]() .
.
∵![]() ,∴
,∴![]() ,∵
,∵![]() ,∴只需要
,∴只需要![]() ,就能使
,就能使![]() 在
在![]() 上是单调递减函数;
上是单调递减函数;
(2)此单调性不能扩展到整个定义域上,这可由单调性定义说明之;
(3)构造函数![]() ,由(1)知当
,由(1)知当![]() 时,
时,![]() 是单调递增函数。∵
是单调递增函数。∵![]() ,∴
,∴![]()
![]() ,∴
,∴![]() ,∴所求解集为
,∴所求解集为![]() .
.

练习册系列答案
相关题目
 ,其中
,其中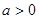 .
. 时,求不等式
时,求不等式 的解集;
的解集; 的解集为
的解集为 ,求
,求 的值.
的值. ,其中
,其中 .
. ,求
,求 在
在 的最小值;
的最小值; 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数 的取值范围;
的取值范围;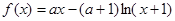 ,其中
,其中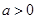
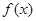 的单调区间;
的单调区间; 时,证明不等式:
时,证明不等式: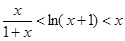 ;
;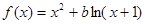 ,其中
,其中 .
.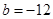 ,求
,求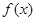 在
在 的最小值;
的最小值; 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数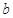 的取值范围;
的取值范围;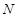 ,使得当
,使得当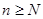 时,不等式
时,不等式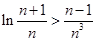 恒成立.
恒成立.