题目内容
已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线l上,过点P作圆M的切线PA,PB,切点为A,B。
(1)若∠APB=60°,求线段AB的长;
(2)当∠APB最大时,求点P的坐标;
(3)求证:经过A、P、M三点的圆必过定点,并求出所有定点的坐标。
(1)若∠APB=60°,求线段AB的长;
(2)当∠APB最大时,求点P的坐标;
(3)求证:经过A、P、M三点的圆必过定点,并求出所有定点的坐标。
解:(1)由题意知,△PAB为等边三角形,所以线段AB的长就是切线长PA,
法一:∵∠APB=60°,由题可知MP=2,
∴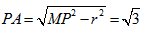 ;
;
法二:∵∠APB=60°,
∴等腰三角形MAB中,∠AMB=120°
而半径MA=1,
∴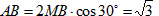 ;
;
(2)记∠APB=2θ,则在直角三角形MAP中,有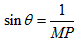 ,
,
当∠APB最大时,有MP最小,此时MP垂直于直线直线l:x-2y=0,
设P(2m,m),
∵M(0,2),
∴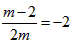 ,
,
∴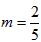 ,
,
∴点P坐标为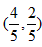 ;
;
(3)设P(2m,m),MP的中点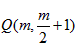 ,因为PA是圆M的切线,
,因为PA是圆M的切线,
所以经过A,P,M三点的圆是以Q为圆心,以MQ为半径的圆,
故其方程为: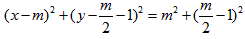
化简得: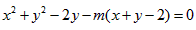 ,
,
此式是关于m的恒等式,
故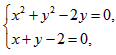 解得
解得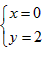 或
或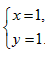 ,
,
所以经过A,P,M三点的圆必过定点(0,2)或(1,1)。
法一:∵∠APB=60°,由题可知MP=2,
∴
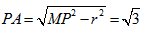 ;
;法二:∵∠APB=60°,
∴等腰三角形MAB中,∠AMB=120°
而半径MA=1,
∴
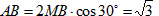 ;
;(2)记∠APB=2θ,则在直角三角形MAP中,有
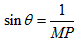 ,
,当∠APB最大时,有MP最小,此时MP垂直于直线直线l:x-2y=0,
设P(2m,m),
∵M(0,2),
∴
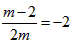 ,
,∴
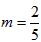 ,
,∴点P坐标为
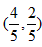 ;
;(3)设P(2m,m),MP的中点
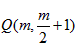 ,因为PA是圆M的切线,
,因为PA是圆M的切线,所以经过A,P,M三点的圆是以Q为圆心,以MQ为半径的圆,
故其方程为:
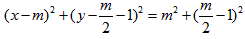
化简得:
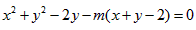 ,
,此式是关于m的恒等式,
故
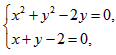 解得
解得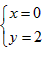 或
或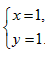 ,
,所以经过A,P,M三点的圆必过定点(0,2)或(1,1)。

练习册系列答案
相关题目
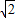 时,求直线CD的方程.
时,求直线CD的方程. 时,求直线CD的方程.
时,求直线CD的方程.