题目内容
设平面向量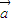 =(x1,y1),
=(x1,y1),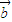 =(x2,y2),定义运算⊙:
=(x2,y2),定义运算⊙: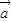 ⊙
⊙ =x1y2-y1x2.已知平面向量
=x1y2-y1x2.已知平面向量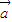 ,
,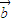 ,
,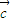 ,则下列说法错误的是( )
,则下列说法错误的是( )A.(
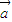 ⊙
⊙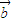 )+(
)+(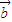 ⊙
⊙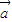 )=0
)=0B.存在非零向量a,b同时满足
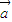 ⊙
⊙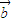 =0且
=0且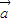 •
•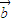 =0
=0C.(
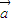 +
+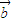 )⊙
)⊙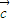 =
=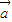 ⊙
⊙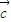 +
+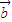 ⊙
⊙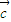
D.|
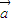 ⊙
⊙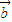 |2=|
|2=|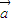 |2|
|2|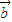 |2-|
|2-|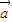 •
•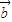 |2
|2
【答案】分析:根据定义不难得出B是错误的,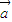 ⊙
⊙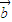 =x1y2-y1x2=0,说明向
=x1y2-y1x2=0,说明向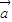 、
、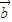 是互相平行的向量,若
是互相平行的向量,若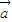 •
•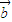 =0,说明它们是垂直的向量.因为不存在两个非零向量,它们既平行又垂直,故B选项是错误的,而对于其它选项,可以分别证明它们是真命题.
=0,说明它们是垂直的向量.因为不存在两个非零向量,它们既平行又垂直,故B选项是错误的,而对于其它选项,可以分别证明它们是真命题.
解答:解:对于A,由定义得,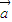 ⊙
⊙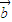 =x1y2-y1x2,
=x1y2-y1x2, ⊙
⊙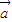 =x2y1-y2x1,所以(
=x2y1-y2x1,所以(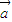 ⊙
⊙ )+(
)+(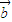 ⊙
⊙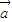 )=0成立,A正确.
)=0成立,A正确.
对于B,因为两个向量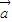 、
、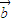 平行的充要条件是x1y2-y1x2=0,若非零向量a,b同时满足
平行的充要条件是x1y2-y1x2=0,若非零向量a,b同时满足 ⊙
⊙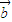 =0且
=0且 •
•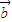 =0,说明两个向量既平行又垂直,故B选项是错误的.
=0,说明两个向量既平行又垂直,故B选项是错误的.
设对于C,设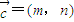 ,则(
,则(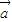 +
+ )⊙
)⊙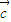 =(x1+x2,y1+y2)⊙
=(x1+x2,y1+y2)⊙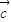 =n(x1+x2)-m(y1+y2)=(nx1-y1m)+(nx2-my2)=
=n(x1+x2)-m(y1+y2)=(nx1-y1m)+(nx2-my2)=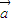 ⊙
⊙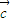 +
+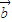 ⊙
⊙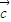 ,故C选项是正确的.
,故C选项是正确的.
对于D,|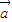 ⊙
⊙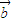 |2=(x1y2-y1x2 )2=x12y22-2x1x2y1y2+y12x22
|2=(x1y2-y1x2 )2=x12y22-2x1x2y1y2+y12x22
|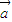 |2|
|2|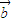 |2-|
|2-|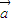 •
•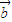 |2=(x12+y12)(x22+y22)-(x1x2+y1y2)2=x12y22-2x1x2y1y2+y12y22,因此D选项是正确的.
|2=(x12+y12)(x22+y22)-(x1x2+y1y2)2=x12y22-2x1x2y1y2+y12y22,因此D选项是正确的.
故选B
点评:本题考查了在新定义下向量数量积的应用,属于基础题.牢记面向量的平行、垂直的充要条件,准确运用它们的坐标运算,是解决本题的关键.
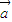 ⊙
⊙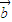 =x1y2-y1x2=0,说明向
=x1y2-y1x2=0,说明向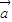 、
、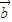 是互相平行的向量,若
是互相平行的向量,若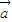 •
•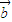 =0,说明它们是垂直的向量.因为不存在两个非零向量,它们既平行又垂直,故B选项是错误的,而对于其它选项,可以分别证明它们是真命题.
=0,说明它们是垂直的向量.因为不存在两个非零向量,它们既平行又垂直,故B选项是错误的,而对于其它选项,可以分别证明它们是真命题.解答:解:对于A,由定义得,
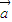 ⊙
⊙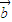 =x1y2-y1x2,
=x1y2-y1x2, ⊙
⊙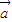 =x2y1-y2x1,所以(
=x2y1-y2x1,所以(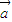 ⊙
⊙ )+(
)+(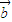 ⊙
⊙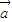 )=0成立,A正确.
)=0成立,A正确.对于B,因为两个向量
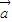 、
、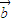 平行的充要条件是x1y2-y1x2=0,若非零向量a,b同时满足
平行的充要条件是x1y2-y1x2=0,若非零向量a,b同时满足 ⊙
⊙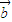 =0且
=0且 •
•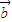 =0,说明两个向量既平行又垂直,故B选项是错误的.
=0,说明两个向量既平行又垂直,故B选项是错误的.设对于C,设
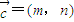 ,则(
,则(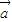 +
+ )⊙
)⊙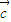 =(x1+x2,y1+y2)⊙
=(x1+x2,y1+y2)⊙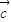 =n(x1+x2)-m(y1+y2)=(nx1-y1m)+(nx2-my2)=
=n(x1+x2)-m(y1+y2)=(nx1-y1m)+(nx2-my2)=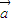 ⊙
⊙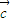 +
+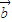 ⊙
⊙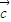 ,故C选项是正确的.
,故C选项是正确的.对于D,|
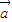 ⊙
⊙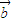 |2=(x1y2-y1x2 )2=x12y22-2x1x2y1y2+y12x22
|2=(x1y2-y1x2 )2=x12y22-2x1x2y1y2+y12x22|
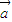 |2|
|2|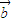 |2-|
|2-|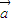 •
•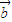 |2=(x12+y12)(x22+y22)-(x1x2+y1y2)2=x12y22-2x1x2y1y2+y12y22,因此D选项是正确的.
|2=(x12+y12)(x22+y22)-(x1x2+y1y2)2=x12y22-2x1x2y1y2+y12y22,因此D选项是正确的.故选B
点评:本题考查了在新定义下向量数量积的应用,属于基础题.牢记面向量的平行、垂直的充要条件,准确运用它们的坐标运算,是解决本题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
设平面向量
=(x1,y1),
=(x2,y2),定义运算⊙:
⊙
=x1y2-y1x2.已知平面向量
,
,
,则下列说法错误的是( )
| a |
| b |
| a |
| b |
| a |
| b |
| c |
A、(
| ||||||||||||||
B、存在非零向量a,b同时满足
| ||||||||||||||
C、(
| ||||||||||||||
D、|
|
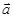 =(x1,y1),
=(x1,y1),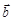 = (x2,y2)
,定义运算⊙:
= (x2,y2)
,定义运算⊙: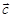 ,则下列说法错误的是
,则下列说法错误的是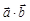 |2
|2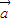 =(x1,y1),
=(x1,y1),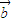 =(x2,y2),定义运算⊙:
=(x2,y2),定义运算⊙: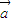 ⊙
⊙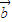 =x1y2-y1x2.已知平面向量
=x1y2-y1x2.已知平面向量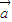 ,
,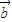 ,
,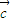 ,则下列说法错误的是( )
,则下列说法错误的是( )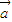 ⊙
⊙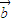 )+(
)+(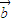 ⊙
⊙ )=0
)=0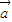 ⊙
⊙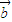 =0且
=0且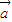 •
•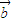 =0
=0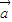 +
+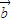 )⊙
)⊙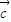 =
=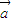 ⊙
⊙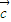 +
+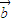 ⊙
⊙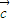
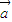 ⊙
⊙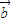 |2=|
|2=|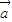 |2|
|2|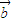 |2-|
|2-|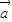 •
•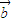 |2
|2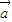 =(x1,y1),
=(x1,y1),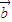 =(x2,y2),定义运算⊙:
=(x2,y2),定义运算⊙: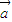 ⊙
⊙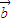 =x1y2-y1x2.已知平面向量
=x1y2-y1x2.已知平面向量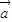 ,
,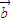 ,
,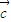 ,则下列说法错误的是( )
,则下列说法错误的是( )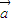 ⊙
⊙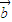 )+(
)+(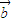 ⊙
⊙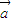 )=0
)=0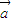 ⊙
⊙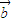 =0且
=0且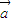 •
•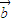 =0
=0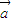 +
+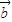 )⊙
)⊙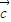 =
=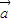 ⊙
⊙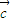 +
+ ⊙
⊙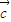
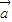 ⊙
⊙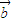 |2=|
|2=|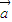 |2|
|2|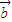 |2-|
|2-|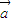 •
•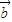 |2
|2