题目内容
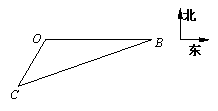
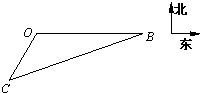 根据气象预报,某海域将有台风,位于港口O(如图)正东方向20海里B处的渔船回港避风时出现故障.位于港口南偏西30°,距港口10海里C处的拖轮接到海事部门营救信息后以30海里1小时的速度沿直线CB去营救渔船,则拖轮到达B处需要
根据气象预报,某海域将有台风,位于港口O(如图)正东方向20海里B处的渔船回港避风时出现故障.位于港口南偏西30°,距港口10海里C处的拖轮接到海事部门营救信息后以30海里1小时的速度沿直线CB去营救渔船,则拖轮到达B处需要分析:由题意可得∠BOC=30°+90°=120°,由余弦定理求得 BC 的值,用距离除以速度,即得拖轮到达B处需要的时间.
解答:解:由题意可得∠BOC=30°+90°=120°,△BOC中,
由余弦定理可得BC=
=10
,
则拖轮到达B处需要的时间为 10
÷30=
小时,
故答案为
.
由余弦定理可得BC=
| 102+202-2×10×20×cos120° |
| 7 |
则拖轮到达B处需要的时间为 10
| 7 |
| ||
| 3 |
故答案为
| ||
| 3 |
点评:本题考查余弦定理的应用,求得∠BOC 的值以及 BC 的值,是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
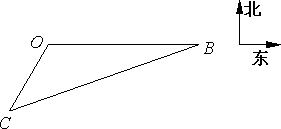
 根据气象预报,某海域将有台风,位于港口O(如图)正东方向20海里B处的渔船回港避风时出现故障.位于港口南偏西30°,距港口10海里C处的拖轮接到海事部门营救信息后以30海里1小时的速度沿直线CB去营救渔船,则拖轮到达B处需要________小时.
根据气象预报,某海域将有台风,位于港口O(如图)正东方向20海里B处的渔船回港避风时出现故障.位于港口南偏西30°,距港口10海里C处的拖轮接到海事部门营救信息后以30海里1小时的速度沿直线CB去营救渔船,则拖轮到达B处需要________小时.