题目内容
设F1、F2分别是双曲线x2- =1的左、右焦点.若点P在双曲线上,且
=1的左、右焦点.若点P在双曲线上,且 •
• =0,则|
=0,则| +
+ |=
|=
- A.

- B.2

- C.

- D.2

B
分析:由点P在双曲线上,且 •
• =0可知|
=0可知| +
+ |=2|
|=2|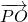 |=|
|=|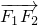 |.由此可以求出|
|.由此可以求出| +
+ |的值.
|的值.
解答:设F1、F2分别是双曲线x2- =1的左、右焦点.
=1的左、右焦点.
∵点P在双曲线上,且 •
• =0,
=0,
∴| +
+ |=2|
|=2|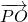 |=|
|=|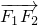 |=2
|=2 .
.
故选B.
点评:把| +
+ |转化为||
|转化为||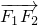 |是正确解题的关键步骤.
|是正确解题的关键步骤.
分析:由点P在双曲线上,且
 •
• =0可知|
=0可知| +
+ |=2|
|=2|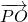 |=|
|=|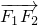 |.由此可以求出|
|.由此可以求出| +
+ |的值.
|的值.解答:设F1、F2分别是双曲线x2-
 =1的左、右焦点.
=1的左、右焦点.∵点P在双曲线上,且
 •
• =0,
=0,∴|
 +
+ |=2|
|=2|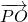 |=|
|=|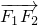 |=2
|=2 .
.故选B.
点评:把|
 +
+ |转化为||
|转化为||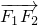 |是正确解题的关键步骤.
|是正确解题的关键步骤. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目