ЬтФПФкШн
ЩшP1(x1ЃЌy1)ЃЌP1(x2ЃЌy2)ЃЌЁЃЌPn(xnЃЌyn)(n³3ЃЌnÎN)ЪЧЖўДЮЧњЯпCЩЯЕФЕуЃЌЧв![]() ЙЙГЩСЫвЛИіЙЋВюd(d¹0)ЕФЕШВюЪ§СаЃЌЦфжаOЪЧзјБъдЕуЃЎМЧSn=a1+a2+Ё+anЃЎ
ЙЙГЩСЫвЛИіЙЋВюd(d¹0)ЕФЕШВюЪ§СаЃЌЦфжаOЪЧзјБъдЕуЃЎМЧSn=a1+a2+Ё+anЃЎ
ЃЈ1ЃЉШєCЕФЗНГЬЮЊ![]() ЃЎЕуP1ЃЈ3ЃЌ0ЃЉМАS3=162ЃЌЧѓЕуP3ЕФзјБъЃЛЃЈжЛашаДГівЛИіЃЉ
ЃЎЕуP1ЃЈ3ЃЌ0ЃЉМАS3=162ЃЌЧѓЕуP3ЕФзјБъЃЛЃЈжЛашаДГівЛИіЃЉ
ЃЈ2ЃЉШєCЕФЗНГЬЮЊy2=2px(p¹0)ЃЎЕуP1(0ЃЌ0)ЃЌЖдгкИјЖЈЕФздШЛЪ§nЃЌжЄУїЃКЃЈx1+pЃЉ2ЃЌ(x2+p)2ЃЌЁЃЌЃЈxn+pЃЉ2ГЩЕШВюЪ§СаЃЛ
ЃЈ3ЃЉШєCЕФЗНГЬЮЊ![]() ЃЎЕуP1(aЃЌ0)ЃЌЖдгкИјЖЈЕФздШЛЪ§nЃЌЕБЙЋВюdБфЛЏЪБЃЌЧѓSnЕФзюаЁжЕЃЎ
ЃЎЕуP1(aЃЌ0)ЃЌЖдгкИјЖЈЕФздШЛЪ§nЃЌЕБЙЋВюdБфЛЏЪБЃЌЧѓSnЕФзюаЁжЕЃЎ
Д№АИЃК
НтЮіЃК
НтЮіЃК
ЃЈ1ЃЉ гЩ ЃЈ2ЃЉЖдУПИіздШЛЪ§kЃЌ1£k£nЃЌгЩЬтвт
Ёр (x1+p)2ЃЌ(x2+p)2ЃЌЁЃЌ(xn+p)2ЪЧЪзЯюЮЊp2,ЙЋВюЮЊdЕФЕШВюЪ§Са. ЃЈ3ЃЉНтЗЈвЛЃКдЕуOЕНЖўДЮЧњЯпCЃК
Ёр ЙЪSnЕФзюаЁжЕЮЊ НтЗЈЖўЃКЖдУПИіздШЛЪ§k(2£k£n)ЃЌ гЩ Ёп
|

СЗЯАВсЯЕСаД№АИ
 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
ЯрЙиЬтФП
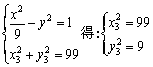 Ёр Еу
Ёр Еу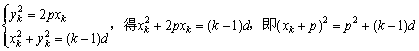
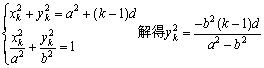
 -y2=1ЃЌn=3ЃЌЕуP1(3ЃЌ0) МАS3=162ЃЌЧѓЕуP3ЕФзјБъЃЛ(жЛашаДГівЛИі)
-y2=1ЃЌn=3ЃЌЕуP1(3ЃЌ0) МАS3=162ЃЌЧѓЕуP3ЕФзјБъЃЛ(жЛашаДГівЛИі)  (aЃОbЃО0)ЃЌЕуP1(aЃЌ0)ЃЌЖдгкИјЖЈЕФздШЛЪ§nЃЌЕБЙЋВюdБфЛЏЪБЃЌЧѓSnЕФзюаЁжЕЁЃ
(aЃОbЃО0)ЃЌЕуP1(aЃЌ0)ЃЌЖдгкИјЖЈЕФздШЛЪ§nЃЌЕБЙЋВюdБфЛЏЪБЃЌЧѓSnЕФзюаЁжЕЁЃ