题目内容
某人在自己的经济林场种植了杨树、沙柳等植物.一次种植了n株沙柳,各株沙柳成活与否是相互独立的,成活率为p,设ξ为成活沙柳的株数,数学期望Eξ=3,标准差σξ为 .
.
(1)求n,p的值
(2)若一株沙柳成活,则一年内通过该株沙柳获利100元,若一株沙柳不能成活,一年内通过该株沙柳损失30元,求一年内该人通过种植沙柳获利的期望.
解:(1)由二项分布的结论:Eξ=np,(σξ)2=np(1-p)
可得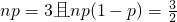 ,
,
得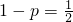 ,从而
,从而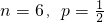
答:n,p的值分别为6和 .
.
(2)设η为该人通过种植沙柳所获得的利润,
则η=100ξ-30(6-ξ)=130ξ-180
所以:Eη=130Eξ-180=210
答:一年内该人通过种植沙柳获利的期望约为210.
分析:(1)根据题意,这是一个n次独立重复试验的模型,其随机变量的分布服从二项分布.根据教材中的结论:二项分布的数学期望为Eξ=np,方差等于Dξ=np(1-p),再结合题中所给的数据解方程组,可得n,p的值;
(2)结合公式η=100ξ-30(n-ξ)=130ξ-30n,再根据(1)的计算结果,最终可得获利的期望为Eη=130Eξ-180
=210.
点评:本题以二项分布与n次独立重复试验的模型为载体,着重考查了离散型随机变量的期望与方差的有关公式等知识点,属于中档题.本题运用的公式较多,请同学们注意加强记忆.
可得
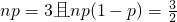 ,
,得
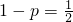 ,从而
,从而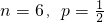
答:n,p的值分别为6和
 .
.(2)设η为该人通过种植沙柳所获得的利润,
则η=100ξ-30(6-ξ)=130ξ-180
所以:Eη=130Eξ-180=210
答:一年内该人通过种植沙柳获利的期望约为210.
分析:(1)根据题意,这是一个n次独立重复试验的模型,其随机变量的分布服从二项分布.根据教材中的结论:二项分布的数学期望为Eξ=np,方差等于Dξ=np(1-p),再结合题中所给的数据解方程组,可得n,p的值;
(2)结合公式η=100ξ-30(n-ξ)=130ξ-30n,再根据(1)的计算结果,最终可得获利的期望为Eη=130Eξ-180
=210.
点评:本题以二项分布与n次独立重复试验的模型为载体,着重考查了离散型随机变量的期望与方差的有关公式等知识点,属于中档题.本题运用的公式较多,请同学们注意加强记忆.

练习册系列答案
相关题目
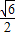 .
.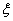 为成活沙柳的株数,数学期望
为成活沙柳的株数,数学期望 ,标准差
,标准差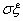 为
为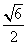 。
。