题目内容
对任意x1,x2∈R,当x1≠x2时,函数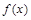 都满足不等式
都满足不等式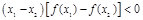 ,若函数
,若函数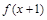 为奇函数,则不等式
为奇函数,则不等式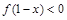 的解集为 ( )
的解集为 ( )
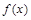 都满足不等式
都满足不等式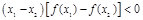 ,若函数
,若函数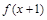 为奇函数,则不等式
为奇函数,则不等式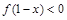 的解集为 ( )
的解集为 ( )A. | B. |
C. | D. |
A
分析:先利用不等式(x1-x2)[f(x1)-f(x2)]<0恒成立得到函数f(x)是定义在R上的减函数;再利用函数f(x+1)是定义在R上的奇函数得到函数f(x)过(1,0)点,二者相结合即可求出不等式f(1-x)<0的解集.
解:由不等式(x1-x2)[f(x1)-f(x2)]<0恒成立得,函数f(x)是定义在R上的减函数 ①.
又因为函数f(x+1)是定义在R上的奇函数,所以有函数f(x+1)过点(0,0);
故函数f(x)过点(1,0)②.
①②相结合得:x>1时,f(x)<0.
故不等式f(1-x)<0转化为1-x>1?x<0.
故选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
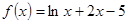 的零点个数为
的零点个数为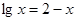 的解为
的解为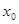 ,则下列说法正确的是( )
,则下列说法正确的是( )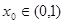
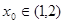
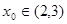
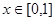
 是方程
是方程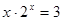 的根,
的根,  是方程
是方程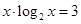 的根,则
的根,则 的值为( )
的值为( )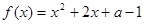 没有零点,则实数
没有零点,则实数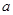 的取值范围为( )
的取值范围为( )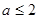
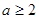
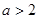
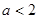
 函数在[a,b]上为单调函数,则 ( )
函数在[a,b]上为单调函数,则 ( )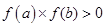

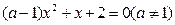 有两个异号实根的一个充分不必要条件是 ( )
有两个异号实根的一个充分不必要条件是 ( )



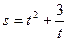 (t是时间,s是位移),则该机器人在时刻
(t是时间,s是位移),则该机器人在时刻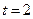 时的瞬时速度为( )
时的瞬时速度为( )



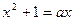 有正实数根,则实数
有正实数根,则实数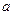 的取值范围是 ▲ ;
的取值范围是 ▲ ;