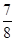题目内容
已知函数f(x)=2
sin2
+sinx-
+1.
(Ⅰ)求f(
)的值;
(Ⅱ)求f(x)的单调递增区间;
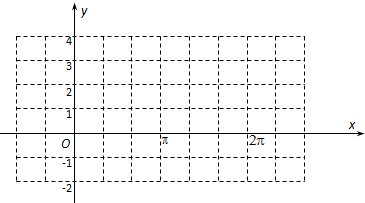
(Ⅲ)作出f(x)在一个周期内的图象.
| 3 |
| x |
| 2 |
| 3 |
(Ⅰ)求f(
| π |
| 3 |
(Ⅱ)求f(x)的单调递增区间;
(Ⅲ)作出f(x)在一个周期内的图象.

(Ⅰ)由已知f(
)=2
sin2
+sin
-
+1…(2分)
=
+
-
+1=1.…(4分)
(Ⅱ)∵f(x)=
(1-cosx)+sinx-
+1…(6分)
=sinx-
cosx+1=2sin(x-
)+1.…(7分)
∵函数y=sinx的单调递增区间为[2kπ-
,2kπ+
](k∈Z),…(8分)
由2kπ-
≤x-
≤2kπ+
,得2kπ-
≤x≤2kπ+
.
所以f(x)的单调递增区间为[2kπ-
,2kπ+
](k∈Z).…(9分)
(Ⅲ)列表:
作出f(x)在一个周期[
,
]上的图象如图所示.…(12分)

| π |
| 3 |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 3 |
=
| ||
| 2 |
| ||
| 2 |
| 3 |
(Ⅱ)∵f(x)=
| 3 |
| 3 |
=sinx-
| 3 |
| π |
| 3 |
∵函数y=sinx的单调递增区间为[2kπ-
| π |
| 2 |
| π |
| 2 |
由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
所以f(x)的单调递增区间为[2kπ-
| π |
| 6 |
| 5π |
| 6 |
(Ⅲ)列表:
| x |
|
|
|
|
| ||||||||||
x-
| 0 |
| π |
| 2π | ||||||||||
2sin(x-
| 0 | 2 | 0 | -2 | 0 |
| π |
| 3 |
| 7π |
| 3 |


练习册系列答案
相关题目
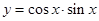 是( ).
是( ). ,则
,则 的值等于( )
的值等于( )




 写成
写成 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标; 满足
满足 ,且边
,且边 所对的角为
所对的角为 ,试求
,试求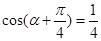 ,则
,则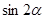 的值为 ( ).
的值为 ( ).