题目内容
已知函数f(x)同时满足如下三个条件:①定义域为[-1,1];②f(x)是偶函数;③x∈[-1,0]时,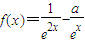 ,其中a∈R.
,其中a∈R.(Ⅰ)求f(x)在[0,1]上的解析式,并求出函数f(x)的最大值;
(Ⅱ)当a≠0,x∈[0,1]时,函数
 ,若g(x)的图象恒在直线y=e上方,求实数a的取值范围(其中e为自然对数的底数,e=2.71828…).
,若g(x)的图象恒在直线y=e上方,求实数a的取值范围(其中e为自然对数的底数,e=2.71828…).
【答案】分析:(Ⅰ)因为函数为偶函数,所以f(x)=f(-x).x∈[-1,0]时,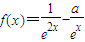 得到x∈[0,1]时得到f(x)的解析式,并讨论a的取值利用二次函数求最值的方法求出最值即可;
得到x∈[0,1]时得到f(x)的解析式,并讨论a的取值利用二次函数求最值的方法求出最值即可;
(Ⅱ)化简g(x),要证g(x)的图象恒在直线y=e上方即就是要证gmin(x)>e成立,利用导数研究函数增减性得到函数的最小值,让其大于e,求出a的范围即可.
解答:解:(Ⅰ)任取x∈[0,1], ,
,
又f(x)是偶函数,故x∈[0,1]时,f(x)=f(-x)=e2x-aex.
由f(x)是定义域为[-1,1]的偶函数可知,f(x)在x∈[0,1]的最大值即可为f(x)的最大值.
当x∈[0,1]时,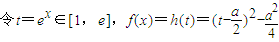
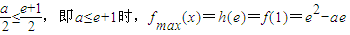 ;
;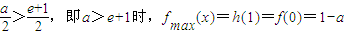 ;
;
综上可知:
a≤e+1时,fmax(x)=f(1)=e2-ae;a>e+1时,fmax(x)=f(0)=1-a.
(Ⅱ)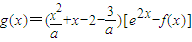
=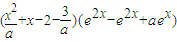 =
=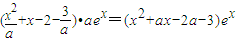
要x∈[0,1]时,函数g(x)的图象恒在直线y=e上方,
即x∈[0,1]时,gmin(x)>e成立,
g′(x)f'(x)=(x+a+3)(x-1)ex,令g′(x)=0,解得x1=-a-3,x2=1
①当-a-3≤0,即a≥-3且a≠0时,可得x∈[0,1]时g′(x)≤0,故g(x)在区间[0,1]单调递减.
此时gmin(x)=g(1)=(-2-a)e>e⇒a<-3,与a≥-3且a≠0矛盾.
②当0<-a-3<1,即-4<a<-3时,可得x∈[0,-a-3]时,g′(x)≥0,x∈[-a-3,1]时g′(x)≤0,可知f(x)在区间[0,-a-3]单调递增.在区间[-a-3,1]单调递减.
此时gmin(x)>e?g(0)>e,且g(1)>e,

故-4<a<-3时可满足题意;
③-a-3≥1,即a≤-4时,可得x∈[0,1]时g′(x)≥0,可知g(x)在区间[0,1]单调递增.
此时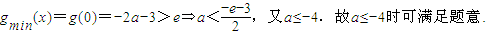
综上可知:a<-3时,g(x)的图象恒在直线y=e上方.
点评:考查学生利用导数求函数最值的能力,以及单调性与奇偶性的综合应用能力,理解不等式恒成立的条件.
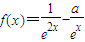 得到x∈[0,1]时得到f(x)的解析式,并讨论a的取值利用二次函数求最值的方法求出最值即可;
得到x∈[0,1]时得到f(x)的解析式,并讨论a的取值利用二次函数求最值的方法求出最值即可;(Ⅱ)化简g(x),要证g(x)的图象恒在直线y=e上方即就是要证gmin(x)>e成立,利用导数研究函数增减性得到函数的最小值,让其大于e,求出a的范围即可.
解答:解:(Ⅰ)任取x∈[0,1],
 ,
,又f(x)是偶函数,故x∈[0,1]时,f(x)=f(-x)=e2x-aex.
由f(x)是定义域为[-1,1]的偶函数可知,f(x)在x∈[0,1]的最大值即可为f(x)的最大值.
当x∈[0,1]时,
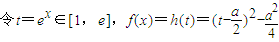
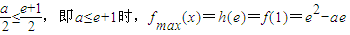 ;
;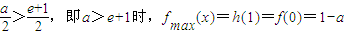 ;
;综上可知:
a≤e+1时,fmax(x)=f(1)=e2-ae;a>e+1时,fmax(x)=f(0)=1-a.
(Ⅱ)
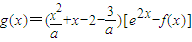
=
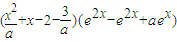 =
=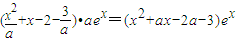
要x∈[0,1]时,函数g(x)的图象恒在直线y=e上方,
即x∈[0,1]时,gmin(x)>e成立,
g′(x)f'(x)=(x+a+3)(x-1)ex,令g′(x)=0,解得x1=-a-3,x2=1
①当-a-3≤0,即a≥-3且a≠0时,可得x∈[0,1]时g′(x)≤0,故g(x)在区间[0,1]单调递减.
此时gmin(x)=g(1)=(-2-a)e>e⇒a<-3,与a≥-3且a≠0矛盾.
②当0<-a-3<1,即-4<a<-3时,可得x∈[0,-a-3]时,g′(x)≥0,x∈[-a-3,1]时g′(x)≤0,可知f(x)在区间[0,-a-3]单调递增.在区间[-a-3,1]单调递减.
此时gmin(x)>e?g(0)>e,且g(1)>e,

故-4<a<-3时可满足题意;
③-a-3≥1,即a≤-4时,可得x∈[0,1]时g′(x)≥0,可知g(x)在区间[0,1]单调递增.
此时
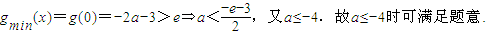
综上可知:a<-3时,g(x)的图象恒在直线y=e上方.
点评:考查学生利用导数求函数最值的能力,以及单调性与奇偶性的综合应用能力,理解不等式恒成立的条件.

练习册系列答案
相关题目
 ,其中a∈R.
,其中a∈R. ,若g(x)的图象恒在直线y=e上方,求实数a的取值范围(其中e为自然对数的底数,e=2.71828…).
,若g(x)的图象恒在直线y=e上方,求实数a的取值范围(其中e为自然对数的底数,e=2.71828…).