题目内容
 如图的曲线是幂函数y=xn在第一象限内的图象.已知n分别取±2,±
如图的曲线是幂函数y=xn在第一象限内的图象.已知n分别取±2,±| 1 |
| 2 |
分析:由题中条件:“n取±2,±
四个值”,依据幂函数y=xn的性质,在第一象限内的图象特征可得.
| 1 |
| 2 |
解答:解:根据幂函数y=xn的性质,在第一象限内的图象,
当n>0时,n越大,递增速度越快,
故曲线c1的n=2,曲线c2的n=
,
当n<0时,|n|越大,曲线越陡峭,所以曲线c3的n=-
,
曲线c4的-2,
故依次填2,
,-
,-2.
故选A.
当n>0时,n越大,递增速度越快,
故曲线c1的n=2,曲线c2的n=
| 1 |
| 2 |
当n<0时,|n|越大,曲线越陡峭,所以曲线c3的n=-
| 1 |
| 2 |
曲线c4的-2,
故依次填2,
| 1 |
| 2 |
| 1 |
| 2 |
故选A.
点评:幂函数是重要的基本初等函数模型之一.学习幂函数重点是掌握幂函数的图形特征,即图象语言,熟记幂函数的图象、性质,把握幂函数的关键点(1,1)和利用直线y=x来刻画其它幂函数在第一象限的凸向.

练习册系列答案
相关题目
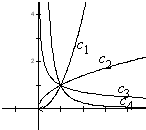
 四个值,与曲线c1、c2、c3、c4相应的n依次为( )
四个值,与曲线c1、c2、c3、c4相应的n依次为( )




 四个值,与曲线c1、c2、c3、c4相应的n依次为( )
四个值,与曲线c1、c2、c3、c4相应的n依次为( )


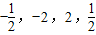

 四个值,与曲线c1、c2、c3、c4相应的n依次为( )
四个值,与曲线c1、c2、c3、c4相应的n依次为( )



