题目内容
双曲线x2-4y2=4的两个焦点F1、F2,P是双曲线上的一点,满足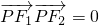 ,则△F1PF2的面积为
,则△F1PF2的面积为
- A.1
- B.

- C.2
- D.

A
分析:根据所给的双曲线的方程,写出双曲线的实轴长和焦点之间的距离,设出要用的点到两个焦点之间的距离,根据双曲线的定义和勾股定理写出m,n之间的关系,求出面积.
解答:∵双曲线x2-4y2=4,
∴a=2,c=
设PF1=m,PF2=n,
∵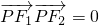 ,
,
∴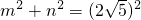 ①
①
m-n=4 ②,
把②平方,然后把①代入,得到mn=2,
∴△F1PF2的面积为 mn=1,
mn=1,
故选A.
点评:本题考查双曲线的定义,解题的关键是根据勾股定理和双曲线的定义,得到表示面积的代数式的值,求出面积.
分析:根据所给的双曲线的方程,写出双曲线的实轴长和焦点之间的距离,设出要用的点到两个焦点之间的距离,根据双曲线的定义和勾股定理写出m,n之间的关系,求出面积.
解答:∵双曲线x2-4y2=4,
∴a=2,c=

设PF1=m,PF2=n,
∵
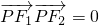 ,
,∴
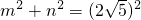 ①
①m-n=4 ②,
把②平方,然后把①代入,得到mn=2,
∴△F1PF2的面积为
 mn=1,
mn=1,故选A.
点评:本题考查双曲线的定义,解题的关键是根据勾股定理和双曲线的定义,得到表示面积的代数式的值,求出面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目