题目内容
已知过点A(-4,0)的动直线l与抛物线G:x2=2py(p>0)相交于B、C两点.当直线l的斜率是
时,
=4
.求抛物线G的方程.
| 1 |
| 2 |
| AC |
| AB |
分析:确定l的方程与抛物线方程联立,利用韦达定理,结合
=4
,即可求得抛物线G的方程.
| AC |
| AB |
解答:解:设B(x1,y1),C(x2,y2),
当直线l的斜率是
时,l的方程为y=
(x+4),即x=2y-4.
与抛物线方程联立得2y2-(8+p)y+8=0,
∴
又∵
=4
,∴y2=4y1,解得:y1=1,y2=4,p=2,
∴抛物线G的方程为x2=4y.
当直线l的斜率是
| 1 |
| 2 |
| 1 |
| 2 |
与抛物线方程联立得2y2-(8+p)y+8=0,
∴
|
又∵
| AC |
| AB |
∴抛物线G的方程为x2=4y.
点评:本题考查直线与抛物线的位置关系,考查向量知识的运用,考查韦达定理,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
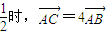 .
.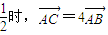 .
.