题目内容
在我国古运河上建有许多形状相同的抛物线型拱桥 (从上游到下游标记,n=0,1,2……),经测量知,相邻两桥之间的距离
(从上游到下游标记,n=0,1,2……),经测量知,相邻两桥之间的距离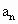 近似地满足
近似地满足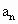 =800+150n(n=1,2,……)这些拱桥当水面距拱顶5m时,桥洞水面宽8m,每年汛期,船公都要考虑拱桥的通行问题,一只装有货物的船,露出水面部分的高为
=800+150n(n=1,2,……)这些拱桥当水面距拱顶5m时,桥洞水面宽8m,每年汛期,船公都要考虑拱桥的通行问题,一只装有货物的船,露出水面部分的高为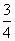 m,宽为4m.
m,宽为4m.
(1)要使该船能顺利通过拱桥,试问水面距拱顶的高度必须达到几米?
(2)已知河水每小时上涨0.15m,船在静水中的速度为0.4m/s,水流速度为15m/min,若船从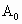 桥起锚顺水航行时,河水开始上涨,试问船将在哪一座桥可能受阻?(
桥起锚顺水航行时,河水开始上涨,试问船将在哪一座桥可能受阻?(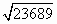 ≈153.9,
≈153.9,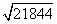 ≈147.8,
≈147.8,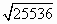 ≈159.9)
≈159.9)
答案:
解析:
解析:
|
解(1)取抛物线型拱桥的拱顶为坐标原点,拱桥的对称轴所在直线为y轴,建立直角坐标系. 设当水面上涨到与抛物线拱顶相距h米时,船不能通行. 设抛物线方程为 ∵A(4,-5)在此抛物线上, ∴P=1.6,抛物线方程为 当船不能通行时,船宽等于 将x=2代入方程得 ∴h=| 因此,水面距拱顶至少2米,船才能顺利通过桥. (2)河水水面由距离拱离5米上升到2米需 船顺水航行速度v=1440+900=2340米/小时,在这段时间内,船航行的路线 d=2340×20=46800米. 由 解得n= 故取n=19时,此时43700= |

练习册系列答案
相关题目
 =-2py(p>0)
=-2py(p>0) ,B点横坐标为2,问题转化为求抛物线
,B点横坐标为2,问题转化为求抛物线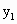 ,然后求h
,然后求h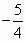
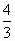 =2.
=2. =20小时.
=20小时. 桥到
桥到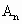 桥的距离
桥的距离 =
=
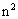 +1750n=46800×2,
+1750n=46800×2,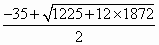 ≈19.8,
≈19.8, <d<
<d<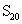 =47350, ∴船在
=47350, ∴船在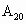 桥受阻.
桥受阻.