题目内容
(1)证明:对?x>0,lnx≤x-1;(2)数列{an},若存在常数M>0,?n∈N*,都有an<M,则称数列{an}有上界.已知
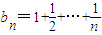 ,试判断数列{bn}是否有上界.
,试判断数列{bn}是否有上界.
【答案】分析:(1)先设g(x)=lnx-(x-1)=lnx-x+1,利用导数研究它的单调性,得出g(x)在x=1处取最大值,即可证得结论;
(2)假设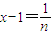 ,从而得出
,从而得出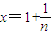 ,由(1)得
,由(1)得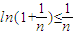 ,即
,即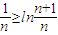 ,再利用?M>0,取n为任意一个不小于eM的自然数,则
,再利用?M>0,取n为任意一个不小于eM的自然数,则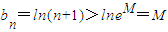 ,从而得出数列{bn}无上界.
,从而得出数列{bn}无上界.
解答:证:(1)设g(x)=lnx-(x-1)=lnx-x+1,?x>0.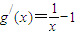 …(1分),
…(1分),
解g′(x)=0得x=1…(2分).
当0<x<1时,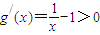 ,g(x)单调递增…(3分);
,g(x)单调递增…(3分);
当x>1时,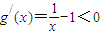 ,g(x)单调递减…(4分),
,g(x)单调递减…(4分),
所以g(x)在x=1处取最大值,即?x>0,g(x)≤g(1)=ln1-1+1=0,lnx≤x-1…(6分)
(2)数列{bn}无上界…(7分)?n∈N*,设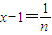 …(8分),
…(8分),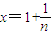 ,
,
由(1)得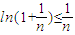 ,
,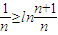 …(10分),
…(10分),
所以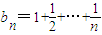
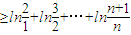 =ln(n+1)…(13分),
=ln(n+1)…(13分),
?M>0,取n为任意一个不小于eM的自然数,
则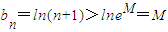 ,数列{bn}无上界…(14分).
,数列{bn}无上界…(14分).
点评:本题主要考查全称命题、数列的通项公式在求解中的应用,及利用导数研究函数的单调性,属于中档题.
(2)假设
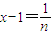 ,从而得出
,从而得出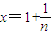 ,由(1)得
,由(1)得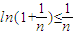 ,即
,即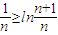 ,再利用?M>0,取n为任意一个不小于eM的自然数,则
,再利用?M>0,取n为任意一个不小于eM的自然数,则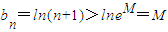 ,从而得出数列{bn}无上界.
,从而得出数列{bn}无上界.解答:证:(1)设g(x)=lnx-(x-1)=lnx-x+1,?x>0.
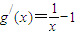 …(1分),
…(1分),解g′(x)=0得x=1…(2分).
当0<x<1时,
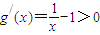 ,g(x)单调递增…(3分);
,g(x)单调递增…(3分);当x>1时,
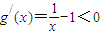 ,g(x)单调递减…(4分),
,g(x)单调递减…(4分),所以g(x)在x=1处取最大值,即?x>0,g(x)≤g(1)=ln1-1+1=0,lnx≤x-1…(6分)
(2)数列{bn}无上界…(7分)?n∈N*,设
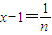 …(8分),
…(8分),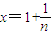 ,
,由(1)得
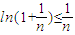 ,
,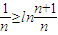 …(10分),
…(10分),所以
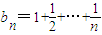
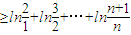 =ln(n+1)…(13分),
=ln(n+1)…(13分),?M>0,取n为任意一个不小于eM的自然数,
则
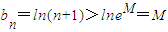 ,数列{bn}无上界…(14分).
,数列{bn}无上界…(14分).点评:本题主要考查全称命题、数列的通项公式在求解中的应用,及利用导数研究函数的单调性,属于中档题.

练习册系列答案
相关题目