题目内容
已知点O为△ABC外接圆的圆心,且 由
由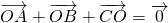 ,则△ABC的内角A等于
,则△ABC的内角A等于
- A.30°
- B.60°
- C.90°
- D.120°
A
分析:根据三个向量之和是零向量,把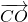 移项,得到两个向量的和等于
移项,得到两个向量的和等于 ,由O为△ABC外接圆的圆心结合向量加法的几何意义知四边形OACB为菱形,得到要求的角.
,由O为△ABC外接圆的圆心结合向量加法的几何意义知四边形OACB为菱形,得到要求的角.
解答: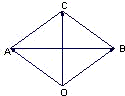 由
由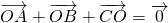
∴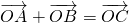 ,
,
如图由O为△ABC外接圆的圆心
结合向量加法的几何意义知四边形OACB为菱形,
∴∠CAO=60°,
∴△ABC的内角A等于30°
故选A.
点评:本题考查向量加减混合运算及其几何意义,考查三角形的外接圆的圆心的性质,是一个平面向量与平面几何的综合题目,题目的运算量比较小,是一个基础题.
分析:根据三个向量之和是零向量,把
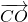 移项,得到两个向量的和等于
移项,得到两个向量的和等于 ,由O为△ABC外接圆的圆心结合向量加法的几何意义知四边形OACB为菱形,得到要求的角.
,由O为△ABC外接圆的圆心结合向量加法的几何意义知四边形OACB为菱形,得到要求的角.解答:
 由
由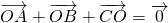
∴
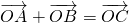 ,
,如图由O为△ABC外接圆的圆心
结合向量加法的几何意义知四边形OACB为菱形,
∴∠CAO=60°,
∴△ABC的内角A等于30°
故选A.
点评:本题考查向量加减混合运算及其几何意义,考查三角形的外接圆的圆心的性质,是一个平面向量与平面几何的综合题目,题目的运算量比较小,是一个基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 平面ABC的充分条件是 ( )
平面ABC的充分条件是 ( ) ;
B.
;
B. ;
; ;
D.
;
D.