Question

设m、n表示直线，α、β表示平面，则下列命题中不正确的是

1. A.
   m⊥α，m⊥β，则α∥β
2. B.
   m∥α，α∩β=n，则m∥n
3. C.
   m⊥α，m∥β，则α⊥β
4. D.
   m∥n，m⊥α，则n⊥α

Answer 1

B
分析：对于命题①③，只要把相应的平面和直线放入长方体中，找到反例即可，对于命题②④，必须根据面面平行的判定和性质定理，给出证明．
解答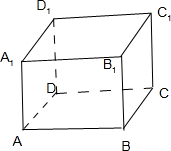：解：A、根据垂直于同一条直线的两个平面平行，故A正确；
B、在长方体ABCD-A₁B₁C₁D₁中
平面AC为平面α，平面AD₁为平面β，直线AD，和直线A₁B₁分别是直线m，n，
C、∵m∥β，∴过直线m的一个平面γ∩β=m′，
则m∥m′
∵m⊥α，∴m′⊥α
∴α⊥β，故C正确．
D、根据线面垂直的性质定理可知选项D正确；
故选B．
点评：此题是个基础题．考查线面的判定和性质定理，要说明一个命题不正确，只需举一个反例即可，特别是定义和定理，一定要弄明白它的内涵和外延，否则给出证明；考查学生灵活应用知识分析解决问题的能力．