题目内容
如图,已知△AOB中,OA=b,OB=a,∠AOB=θ(a≥b,θ是锐角),作AB1⊥OB,B1A1∥BA;再作A1B2⊥OB,B2A2∥BA;如此无限连续作下去,设△ABB1,△A1B1B2,…的面积为S1,S2,…求无穷数列S1,S2,…的和.
【答案】分析:首先用a,b,θ表示出AB1和BB1进而表示出△B1AB,进而表示出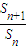 ,发现数列{Sn}为等比数列,公比为
,发现数列{Sn}为等比数列,公比为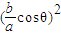 根据其小于1,推断此数列为递缩等比数列.进而通过数列{Sn}的前n项和的极限求得答案.
根据其小于1,推断此数列为递缩等比数列.进而通过数列{Sn}的前n项和的极限求得答案.
解答:解:AB1=bsinθ,BB1=a-bcosθ
(对一切n≥1成立,此时视AB为AB)
∵△ABB1∽△A1B1B2∽△A2B2B3∽,
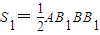 =
= bsinθ(a-bcosθ),
bsinθ(a-bcosθ),
∵△OAB1∽△OA1B1∽△OA2B2…
∴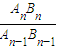 =
=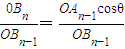 =
=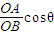 =
=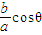 ,
,
∴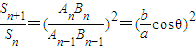 ,
,
即公比Q=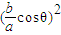 .
.
∵θ是锐角,a≥b,
∴0<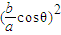 <1,
<1,
∴数列S1,S2,S3,是无穷递缩等比数列,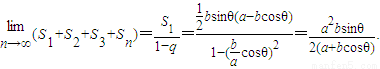
点评:本题主要考查了等比数列的求和问题.做题的关键是从题设的条件中归纳出等比数列.
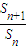 ,发现数列{Sn}为等比数列,公比为
,发现数列{Sn}为等比数列,公比为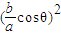 根据其小于1,推断此数列为递缩等比数列.进而通过数列{Sn}的前n项和的极限求得答案.
根据其小于1,推断此数列为递缩等比数列.进而通过数列{Sn}的前n项和的极限求得答案.解答:解:AB1=bsinθ,BB1=a-bcosθ
(对一切n≥1成立,此时视AB为AB)
∵△ABB1∽△A1B1B2∽△A2B2B3∽,
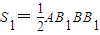 =
= bsinθ(a-bcosθ),
bsinθ(a-bcosθ),∵△OAB1∽△OA1B1∽△OA2B2…
∴
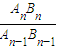 =
=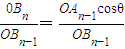 =
=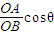 =
=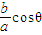 ,
,∴
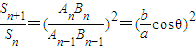 ,
,即公比Q=
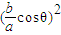 .
.∵θ是锐角,a≥b,
∴0<
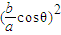 <1,
<1,∴数列S1,S2,S3,是无穷递缩等比数列,
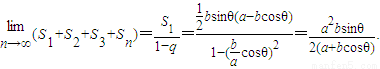
点评:本题主要考查了等比数列的求和问题.做题的关键是从题设的条件中归纳出等比数列.

练习册系列答案
相关题目
 如图,在三角形AOB中,已知∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,求△AOC为钝角三角形的概率.( )
如图,在三角形AOB中,已知∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,求△AOC为钝角三角形的概率.( )| A、0.6 | B、0.4 | C、0.2 | D、0.1 |

 如图所示,已知△AOB中,
如图所示,已知△AOB中,