题目内容
已知函数f(x)= -1(x≥1)的图象是
-1(x≥1)的图象是 ,曲线
,曲线 与
与 关于直线y=x对称.
关于直线y=x对称.
(1)求曲线 的方程y=g(x);
的方程y=g(x);
(2)设函数y=g(x)的定义域为M, ∈M,且
∈M,且 ,求证:|g(
,求证:|g(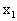 )-g(
)-g( )|<|
)|<| |;
|;
(3)设A,B是曲线 上任意不同两点,证明直线AB与直线y=x必相交.
上任意不同两点,证明直线AB与直线y=x必相交.
答案:
解析:
解析:
|
解 (1)∵曲线 ∴y=g(x)是y=f(x)的反函数,由y= 证 (2)由(1)知M={x|x≥0},设
故 证 (3)设A( |

练习册系列答案
相关题目
 关于直线y=x对称,
关于直线y=x对称,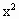 -1,得
-1,得 =y+1,而由x≥1,知y≥0,从而x=
=y+1,而由x≥1,知y≥0,从而x=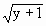 (y≥0),∴曲线
(y≥0),∴曲线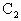 的方程是g(x)=
的方程是g(x)=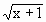 (x≥0).
(x≥0).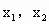 ∈M,且
∈M,且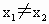 .则有
.则有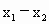 ≠0,
≠0,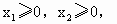
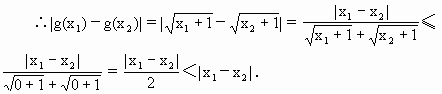
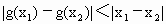 .
.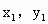 ),B(
),B(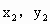 )是曲线
)是曲线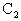 上任意不同两点,
上任意不同两点,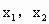 ∈M,且
∈M,且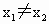 ,由(2)知
,由(2)知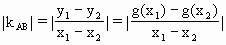 <1,∴直线AB的斜率
<1,∴直线AB的斜率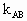 ≠1,又∵直线y=x的斜率为1,∴直线AB与直线y=x必相交.
≠1,又∵直线y=x的斜率为1,∴直线AB与直线y=x必相交. )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有