题目内容
已知函数 (a,b∈R)
(a,b∈R)(1)若y=f(x)图象上的点
 处的切线斜率为-4,求y=f(x)的极大值;
处的切线斜率为-4,求y=f(x)的极大值;(2)若y=f(x)在区间[-1,2]上是单调减函数,求a+b的最小值.
【答案】分析:(1)根据导数的几何意义求出函数f(x)在x=1处的导数,以及切点在图象上建立方程组,解之即可求出a和b求出解析式,先求出f′(x)=0的值,再讨论满足f′(x)=0的点附近的导数的符号的变化情况,来确定极值即可;
(2)将条件“若y=f(x)在区间[-1,2]上是单调减函数”转化成f'(x)=x2+2ax-b≤0在区间[-1,2]上恒成立,根据二次函数图象建立约束条件,利用线性规划的方法求出a+b的最小值即可.
解答:解:(1)∵f'(x)=x2+2ax-b,
∴由题意可知:f'(1)=-4且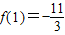 ,
,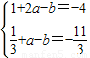
解得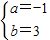 (3分)
(3分)
∴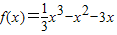
f'(x)=x2-2x-3=(x+1)(x-3)
令f'(x)=0,得x1=-1,x2=3
由此可知:

∴当x=-1时,f(x)取极大值 .(6分)
.(6分)
(2)∵y=f(x)在区间[-1,2]上是单调减函数,
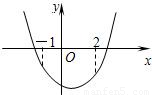
∴f'(x)=x2+2ax-b≤0在区间[-1,2]上恒成立.
根据二次函数图象可知f'(-1)≤0且f'(2)≤0,
即: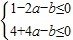
也即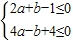 (9分)
(9分)
作出不等式组表示的平面区域如图:
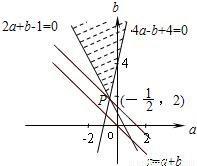
当直线z=a+b经过交点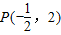 时,z=a+b取得最小值
时,z=a+b取得最小值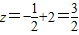 ,
,
∴z=a+b取得最小值为 (12分)
(12分)
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数的单调性和线性规划的应用,属于基础题.
(2)将条件“若y=f(x)在区间[-1,2]上是单调减函数”转化成f'(x)=x2+2ax-b≤0在区间[-1,2]上恒成立,根据二次函数图象建立约束条件,利用线性规划的方法求出a+b的最小值即可.
解答:解:(1)∵f'(x)=x2+2ax-b,
∴由题意可知:f'(1)=-4且
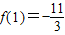 ,
,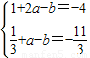
解得
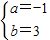 (3分)
(3分)∴
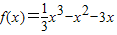
f'(x)=x2-2x-3=(x+1)(x-3)
令f'(x)=0,得x1=-1,x2=3
由此可知:

∴当x=-1时,f(x)取极大值
 .(6分)
.(6分)(2)∵y=f(x)在区间[-1,2]上是单调减函数,
∴f'(x)=x2+2ax-b≤0在区间[-1,2]上恒成立.
根据二次函数图象可知f'(-1)≤0且f'(2)≤0,

即:
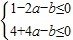
也即
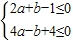 (9分)
(9分)作出不等式组表示的平面区域如图:

当直线z=a+b经过交点
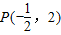 时,z=a+b取得最小值
时,z=a+b取得最小值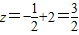 ,
,∴z=a+b取得最小值为
 (12分)
(12分)点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数的单调性和线性规划的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (a,b∈R)
(a,b∈R) 处的切线斜率为-4,求y=f(x)的极大值;
处的切线斜率为-4,求y=f(x)的极大值; (a、b∈R),
(a、b∈R), 为增函数,
为增函数, 为减函数,若存在,求出b的值,若不存在,请说明理由;
为减函数,若存在,求出b的值,若不存在,请说明理由; (a、b∈R),
(a、b∈R), 为增函数,
为增函数, 为减函数,若存在,求出b的值,若不存在,请说明理由;
为减函数,若存在,求出b的值,若不存在,请说明理由;