题目内容
已知坐标平面上三点A(2,0),B(0,2),C(cosα,sinα).(1)若(
| OA |
| OC |
| OB |
| OC |
(2)若
| AC |
| BC |
分析:(1)首先根据(
+
)2=7,求出cosα,再根据向量的积求出夹角即可.
(2)先表示出向量AC和BC,然后根据向量垂直的条件得出,
•
=0,从而求出cosα+sinα=
,然后得出它的平方,进而求得sin2α.
| OA |
| OC |
(2)先表示出向量AC和BC,然后根据向量垂直的条件得出,
| AC |
| BC |
| 1 |
| 2 |
解答:解:(1)∵
+
=(2+cosα,sinα),(
+
)2=7,
∴(2+cosα)2+sin2α=7,
∴cosα=
.
又B(0,2),C(cosα,sinα),设
与
的夹角为θ,
则:cosθ=
=
=sinα=±
,
∴
与
的夹角为
或
π.
(2)解:∵
=(cosα-2,sinα),
=(cosα,sinα-2),
由
⊥
,∴
•
=0,
可得cosα+sinα=
,①
∴(cosα+sinα)2=
,∴2sinαcosα=-
,sin2α=-
| OA |
| OC |
| OA |
| OC |
∴(2+cosα)2+sin2α=7,
∴cosα=
| 1 |
| 2 |
又B(0,2),C(cosα,sinα),设
| OB |
| OC |
则:cosθ=
| ||||
|
|
| 2sinα |
| 2 |
| ||
| 2 |
∴
| OB |
| OC |
| π |
| 6 |
| 5 |
| 6 |
(2)解:∵
| AC |
| BC |
由
| AC |
| BC |
| AC |
| BC |
可得cosα+sinα=
| 1 |
| 2 |
∴(cosα+sinα)2=
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
点评:本题考查了二倍角的正弦,向量垂直的条件等知识,熟练掌握相关公式是解题的关键,属于基础题.

练习册系列答案
相关题目
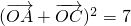 (O为坐标原点),求向量
(O为坐标原点),求向量 与
与 夹角的大小;
夹角的大小; ,当0<α<π时,求tanα的值.
,当0<α<π时,求tanα的值. (O为原点),求向量
(O为原点),求向量 与
与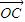 夹角的大小;
夹角的大小; ,求sin2α的值.
,求sin2α的值.