题目内容
已知各项均为正数的数列 满足
满足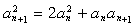 , 且
, 且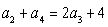 ,其中
,其中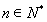 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 设数列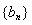 满足
满足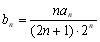 ,是否存在正整数
,是否存在正整数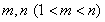 ,使得
,使得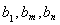 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的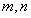 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(3) 令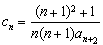 ,记数列
,记数列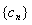 的前
的前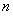 项和为
项和为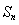 ,其中
,其中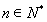 ,证明:
,证明: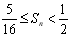 。
。
【答案】
(1)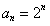 (2)存在且
(2)存在且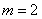 ,
,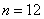
【解析】
试题分析:
(1)利用十字相乘法分解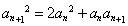 ,得到关于
,得到关于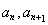 的递推式,证得数学
的递推式,证得数学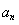 为等比数列且可以知道公比,则把公比带入式子
为等比数列且可以知道公比,则把公比带入式子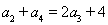 就可以求出首项,进而得到
就可以求出首项,进而得到 的通项公式.
的通项公式.
(2)由第一问可得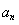 的通项公式带入
的通项公式带入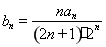 可
可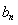 的通项公式,结合
的通项公式,结合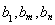 成等比数列,满足等比中项,得到关于m,n的等式,借助m,n都为正整数,利用等式两边的范围求出n,m的范围等到m,n的值.
成等比数列,满足等比中项,得到关于m,n的等式,借助m,n都为正整数,利用等式两边的范围求出n,m的范围等到m,n的值.
(3)由(1)得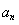 ,带入
,带入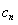 得到
得到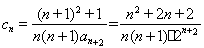 ,由于要得到钱n项和
,由于要得到钱n项和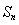 ,故考虑把
,故考虑把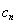 进行分离得到
进行分离得到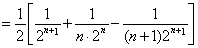 , 进而利用分组求和和裂项求和求的
, 进而利用分组求和和裂项求和求的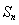
 ,观察
,观察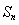 的单调性,可得到
的单调性,可得到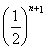 与
与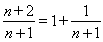 都关于n单调递减,进而得到
都关于n单调递减,进而得到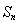 关于n是单调递增的,则有
关于n是单调递增的,则有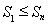 ,再根据
,再根据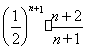 的非负性,即可得到
的非负性,即可得到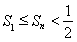 ,进而证明原式.
,进而证明原式.
试题解析:
(1) 因为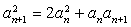 ,即
,即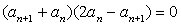 1分
1分
又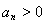 ,所以有
,所以有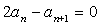 ,即
,即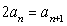 所以数列
所以数列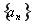 是公比为
是公比为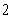 的等比数列. 2分
的等比数列. 2分
由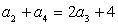 得
得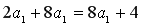 ,解得
,解得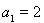 。 3分
。 3分
从而,数列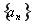 的通项公式为
的通项公式为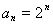
 。 4分
。 4分
(2)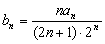 =
=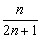 ,若
,若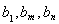 成等比数列,则
成等比数列,则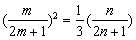 , 5分
, 5分
即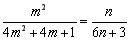 .由
.由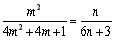 ,可得
,可得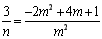 , 6分
, 6分
所以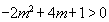 ,解得:
,解得: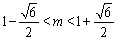 。 7分
。 7分
又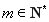 ,且
,且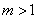 ,所以
,所以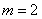 ,此时
,此时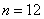 .
.
故当且仅当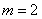 ,
,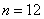 .使得
.使得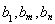 成等比数列。 8分
成等比数列。 8分
(3) 
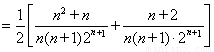
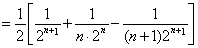 10分
10分
∴ 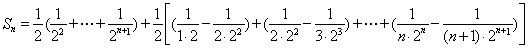
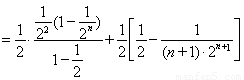
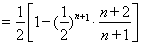 12分
12分
易知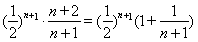 递减,∴0<
递减,∴0<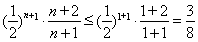 13分
13分
∴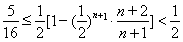 ,即
,即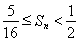 14分
14分
考点:十字相乘法 等比数列 分组求和 裂项求和 不等式 单调性

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明.