题目内容
已知 ,
, 是空间二向量,若
是空间二向量,若 =3,|
=3,| |=2,|
|=2,| -
- |=
|= ,则
,则 与
与 的夹角为________.
的夹角为________.
60°
分析:把| -
- |=
|= 两边平方,整理出两个向量的数量积的值,根据两个向量的夹角的公式,代入两个向量的数量积和两个向量的模长,得到余弦值,根据角的范围得到结果.
两边平方,整理出两个向量的数量积的值,根据两个向量的夹角的公式,代入两个向量的数量积和两个向量的模长,得到余弦值,根据角的范围得到结果.
解答:∵| -
- |=
|= ,
,
∴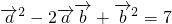
∴ =3,
=3,
∴cos< >=
>=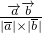 =
=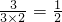
∵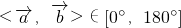
∴ 与
与 的夹角为60°.
的夹角为60°.
故答案为:60°
点评:本题考查平面向量数量积表示夹角和模长,本题解题的关键是整理出两个向量的数量积,再用夹角的表示式.
分析:把|
 -
- |=
|= 两边平方,整理出两个向量的数量积的值,根据两个向量的夹角的公式,代入两个向量的数量积和两个向量的模长,得到余弦值,根据角的范围得到结果.
两边平方,整理出两个向量的数量积的值,根据两个向量的夹角的公式,代入两个向量的数量积和两个向量的模长,得到余弦值,根据角的范围得到结果.解答:∵|
 -
- |=
|= ,
,∴
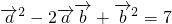
∴
 =3,
=3,∴cos<
 >=
>=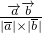 =
=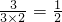
∵
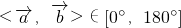
∴
 与
与 的夹角为60°.
的夹角为60°.故答案为:60°
点评:本题考查平面向量数量积表示夹角和模长,本题解题的关键是整理出两个向量的数量积,再用夹角的表示式.

练习册系列答案
相关题目
 中,
中,  ,
, ,
,
 是
是 和
和 的交点, 若
的交点, 若 .
.  的长; (2)求点
的长; (2)求点 到平面
到平面 的距离;
的距离; 的平面角的正弦值的大小.
的平面角的正弦值的大小.
 A
A AC=3
AC=3 BC
BC ,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
 C
C sin
sin , -
, - ) ……………………… 3分
) ……………………… 3分 =(2, -
=(2, - =(0,
-3, -h) ……… 4分
=(0,
-3, -h) ……… 4分 =(a, b, c),则可求得
=(a, b, c),则可求得 |=
|= =(x, y, z),则可求得
=(x, y, z),则可求得 满足cos
满足cos =
= ………
11分
………
11分