题目内容
已知a，b是相交直线，a∥平面α，则b与平面α的位置关系是
- A.相交
- B.平行
- C.相交或平行
- D.b在α内
C
分析：通过线面的位置关系分类讨论即可得到．
解答：如图所示：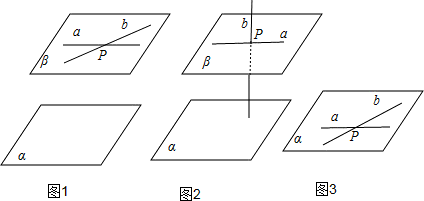
①如图1，若a、b确定的平面β∥α，
则b∥α；
②如图2，若a所在的平面β∥α，但是b∩β=P，则b必与α相交；
③如图3，若b?α，a∩b=P，则点P也必在α内，这与a∥α矛盾．
综上可知：b与平面α的位置关系是相交或平行，但是b不可能在α内．
因此答案是C．
故选C．
点评：熟练掌握线面的位置关系是解题的关键．
分析：通过线面的位置关系分类讨论即可得到．
解答：如图所示：
①如图1，若a、b确定的平面β∥α，
则b∥α；
②如图2，若a所在的平面β∥α，但是b∩β=P，则b必与α相交；
③如图3，若b?α，a∩b=P，则点P也必在α内，这与a∥α矛盾．
综上可知：b与平面α的位置关系是相交或平行，但是b不可能在α内．
因此答案是C．
故选C．
点评：熟练掌握线面的位置关系是解题的关键．
练习册系列答案
相关题目
已知A、B是圆x2+y2=1与x轴的两个交点，CD是垂直于AB的动弦，直线AC和DB相交于点P，问是否存在两个定点E、F，使||PE|-|PF||为定值？若存在，求出E、F的坐标； 若不存在，请说明理由．已知a、b是两条异面直线，c∥a，那么c与b的位置关系（ ）
| A、一定是异面 | B、不可能平行 | C、一定是相交 | D、不可能相交 |