题目内容
在△ABC中,2sin2 =
= sinA,sin(B-C)=2cosBsinC,则
sinA,sin(B-C)=2cosBsinC,则 =____________.
=____________.
 =
= sinA,sin(B-C)=2cosBsinC,则
sinA,sin(B-C)=2cosBsinC,则 =____________.
=____________.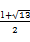
2sin2 =
= sinA?1-cosA=
sinA?1-cosA= sinA?sin
sinA?sin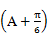 =
= ,
,
又0<A<π,所以 <A+
<A+ <
<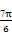 ,
,
所以A+ =
=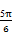 ,所以A=
,所以A=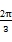 .
.
再由余弦定理,得a2=b2+c2+bc ①
将sin(B-C)=2cosBsinC展开,
得sinBcosC=3cosBsinC,
所以将其角化边,得b·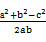
=3·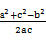 ·c,即2b2-2c2=a2 ②
·c,即2b2-2c2=a2 ②
将①代入②,得b2-3c2-bc=0,
左右两边同除以bc,得 -3×
-3× -1=0, ③
-1=0, ③
解③得 =
=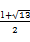 或
或 =
=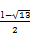 (舍),
(舍),
所以 =
= =
=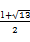 .
.
 =
= sinA?1-cosA=
sinA?1-cosA= sinA?sin
sinA?sin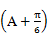 =
= ,
,又0<A<π,所以
 <A+
<A+ <
<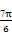 ,
,所以A+
 =
=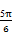 ,所以A=
,所以A=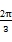 .
.再由余弦定理,得a2=b2+c2+bc ①
将sin(B-C)=2cosBsinC展开,
得sinBcosC=3cosBsinC,
所以将其角化边,得b·
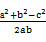
=3·
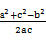 ·c,即2b2-2c2=a2 ②
·c,即2b2-2c2=a2 ②将①代入②,得b2-3c2-bc=0,
左右两边同除以bc,得
 -3×
-3× -1=0, ③
-1=0, ③解③得
 =
=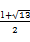 或
或 =
=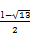 (舍),
(舍),所以
 =
= =
=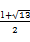 .
.
练习册系列答案
相关题目
 中,已知B=45AD=5,Ac=7,Dc=3
中,已知B=45AD=5,Ac=7,Dc=3 ,
, 是
是 上一点,
上一点, ,求
,求 的长.
的长.
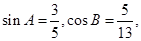 则
则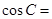 .
.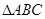 中,角
中,角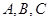 的对边分别为
的对边分别为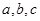 ,若点
,若点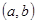 在直线
在直线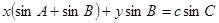 上,则角
上,则角 的值为( )
的值为( )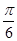 B.
B.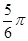
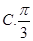
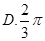
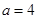 ,
,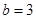 ,
,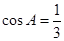 ,则
,则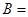 ( )
( )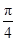
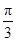
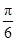
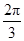
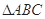 的内角
的内角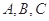 所对边的长分别为
所对边的长分别为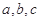 ,若
,若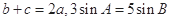 ,则角
,则角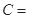 ( )
( )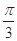
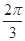
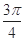
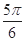
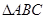 中,角
中,角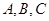 对的边分别为
对的边分别为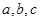 ,已知
,已知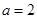 .
.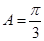 ,求
,求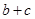 的取值范围;
的取值范围;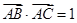 ,求
,求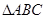 中,
中,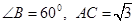 ,则
,则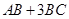 的最大值为 .
的最大值为 .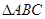 为锐角三角形,
为锐角三角形,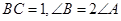 ,则
,则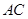 的取值范围为_______.
的取值范围为_______.