题目内容
如图,四棱锥 中,底面
中,底面 是菱形,
是菱形, ,
,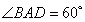 ,
, 是
是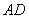 的中点,点
的中点,点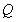 在侧棱
在侧棱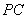 上.
上.

(1)求证: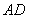 ⊥平面
⊥平面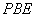 ;
;
(2)若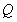 是
是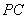 的中点,求证:
的中点,求证: //平面
//平面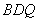 ;
;
(3)若 ,试求
,试求 的值.
的值.
【答案】
(1)详见解析(2)详见解析(3)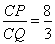
【解析】
试题分析:(1)由线面垂直判定定理,要证线面垂直,需证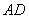 垂直平面
垂直平面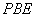 内两条相交直线,由
内两条相交直线,由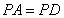 ,
,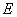 是
是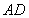 的中点,易得
的中点,易得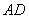 垂直于
垂直于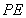 ,再由底面
,再由底面 是菱形,
是菱形,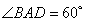 得三角形
得三角形 为正三角形,所以
为正三角形,所以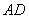 垂直于
垂直于 ,(2)由线面平行判定定理,要证线面平行,需证
,(2)由线面平行判定定理,要证线面平行,需证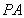 平行于平面
平行于平面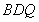 内一条直线,根据
内一条直线,根据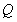 是
是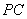 的中点,联想到取AC中点O所以OQ为△PAC中位线.所以OQ // PA注意在写定理条件时,不能省,要全面.例如,线面垂直判定定理中有五个条件,线线垂直两个,相交一个,线在面内两个;线面平行判定定理中有三个条件,平行一个,线在面内一个,线在面外一个,(3)研究体积问题关键在于确定高,由于两个底面共面,所以求
的中点,联想到取AC中点O所以OQ为△PAC中位线.所以OQ // PA注意在写定理条件时,不能省,要全面.例如,线面垂直判定定理中有五个条件,线线垂直两个,相交一个,线在面内两个;线面平行判定定理中有三个条件,平行一个,线在面内一个,线在面外一个,(3)研究体积问题关键在于确定高,由于两个底面共面,所以求 的值就转化为求对应高的长度比.
的值就转化为求对应高的长度比.
试题解析:(1)因为E是AD的中点,PA=PD,所以AD⊥PE.
因为底面ABCD是菱形,∠BAD=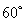 ,所以AB=BD,又因为E是AD的中点,所以 AD⊥BE.
,所以AB=BD,又因为E是AD的中点,所以 AD⊥BE.
因为PE∩BE=E,所以AD⊥平面PBE. 4分
(2)连接AC交BD于点O,连结OQ.因为O是AC中点,
Q是PC的中点,所以OQ为△PAC中位线.所以OQ//PA. 7分
因为PA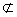 平面BDQ,OQ
平面BDQ,OQ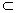 平面BDQ.所以PA//平面BDQ. 9分
平面BDQ.所以PA//平面BDQ. 9分
(3)设四棱锥P-BCDE,Q-ABCD的高分别为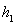 ,
,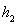 ,所以VP-BCDE=
,所以VP-BCDE=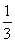 SBCDE
SBCDE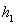 ,VQ-ABCD=
,VQ-ABCD=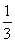 SABCD
SABCD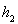 . 10分
. 10分
因为VP-BCDE=2VQ-ABCD,且底面积SBCDE= SABCD. 12分
SABCD. 12分
所以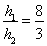 ,因为
,因为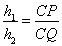 ,所以
,所以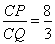 . 14分
. 14分
考点:线面垂直判定定理, 线面平行判定定理,锥的体积.

练习册系列答案
相关题目
 如图,四棱锥中,底面ABCD是菱形,SA=SD=
如图,四棱锥中,底面ABCD是菱形,SA=SD= 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ⊥底面
⊥底面 平面
平面 ;
②若二面角
;
②若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.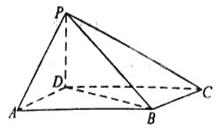
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,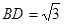 ,
, ⊥底面
⊥底面 平面
平面 ;
;
 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, 底面
底面 ;
; 求二面角
求二面角 的余弦值.
的余弦值.
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,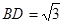 ,
, ⊥底面
⊥底面 平面
平面 ;
;
 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。