Question

证明正方形的对角线互相垂直平分.

Answer 1

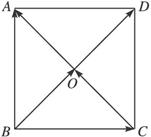
证明：如上图，设一组基底=a，=b，则=a+b.=a-b,

∵·=(a+b)·(a-b)

=a²-b²=|a|²-|b|²=0，

∴⊥,即BD⊥AC.

设AC与BD交于O点，

∵与共线，

∴=λ=λ（a+b）,①

又∵与共线，∴=μ=μ（a-b）,

∵在△BOC中=+.

=b+μa-μb=μa+(1-μ)b②

由①②得：解得λ==μ.

∴AC与BD互相平分.

综上，正方形的对角线垂直且互相平分.