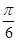题目内容
设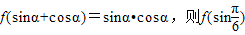 的值为 .
的值为 .
【答案】分析:用换元法求出函数f(x)的解析式,从而可求函数值.
解答:解:令sinα+cosα=t(t∈[-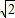 ,
,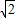 ]),
]),
平方后化简可得 sinαcosα=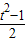 ,
,
再由f(sinα+cosα)=sinαcosα,得f(t)=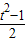 ,
,
所以f(sin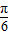 )=f(
)=f( )=
)=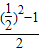 =-
=- .
.
故答案为:- .
.
点评:本题主要考查换元法求函数的解析式,注意换元中变量取值范围的变化,属于基础题.
解答:解:令sinα+cosα=t(t∈[-
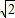 ,
,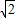 ]),
]),平方后化简可得 sinαcosα=
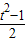 ,
,再由f(sinα+cosα)=sinαcosα,得f(t)=
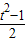 ,
,所以f(sin
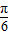 )=f(
)=f( )=
)=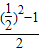 =-
=- .
.故答案为:-
 .
.点评:本题主要考查换元法求函数的解析式,注意换元中变量取值范围的变化,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
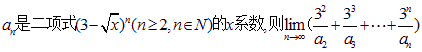 的值为( )
的值为( )
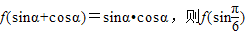 的值为 .
的值为 .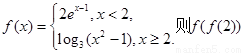 的值为 ( )
的值为 ( ) 的值为 ( )
的值为 ( )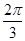 B.
B. C.
C.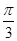 D.
D.