Question

如图在边长为2

2

的正三角形ABC中，D、E、F分别为各边的中点，G、H、I、J分别为AF、AD、BE、DE的中点，若△ABC沿DE、EF、DF折成三棱锥A-DEF以后，以下命题错误的是（　　）

• A．HG与IJ所成角为60°
• B．HG⊥AF
• C．三棱锥A-DEF的体积为

  1

  3

• D．三角形DEF的面积为

  3

Answer 1

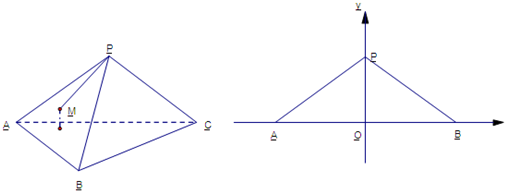
分析：△ABC沿DE，EF，DF折成三棱锥以后，I，J分别为BE、DE的中点，则IJ∥侧棱，故GH与IJ所成角与侧棱与GH所成的角相等．AD为折成三棱锥的侧棱，则GH与IJ所成角的度数为60°；由HG∥BC，AF⊥BC，知HG⊥AF；边长为2

2

的正三角形ABC中，D、E、F分别为各边的中点，能求出三角形DEF的面积和三棱锥A-DEF的体积．

解答：解：将△ABC沿DE，EF，DF折成三棱锥以后，
I、J分别为BE、DE的中点，则IJ∥侧棱，
故GH与IJ所成角与侧棱与GH所成的角相等；
AD为折成三棱锥的侧棱，因为∠AHG=60°，
故GH与IJ所成角的度数为60°，故A正确；
∵HG∥BC，AF⊥BC，∴HG⊥AF，故B正确；
∵边长为2

2

的正三角形ABC中，D、E、F分别为各边的中点，
∴三角形DEF的面积S=

1

2

×

2

×

2

×sin60°=

3

2

，
三棱锥A-DEF的体积V=

1

3

×

3

2

×

2- 2 3

=

1

3

，故C正确，D错误．
故选D．

点评：本题主要考查了两直线所成角，考查了两直线的位置关系的判断，考查了三角形面积和三锥锥体的计算，解题的关键就是弄清翻折后的图形，属于中档题．