题目内容
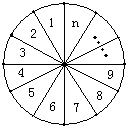
 如图,将圆分成n个区域,用3种不同颜色给每个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为an.
如图,将圆分成n个区域,用3种不同颜色给每个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为an.(1)求a1,a2,a3,a4;
(2)求证:an+an+1=3×2n(n≥2);
(3)求数列{an}的通项公式.
分析:(1)直接求出n=1时a1,n=2时a2,n=3时a3,n=4时a4;的值;
(2)依次对扇形区域染色求出an然后说明它与an+1(n≥2)的关系式:an+an+1=3×2n(n≥2)
(3)由(2)a2+a3=3×22,a3+a4=3×23,…,an-1+an=3×2n-1,将上述n-2个等式两边分别乘以(-1)k,整理计算即可.
(2)依次对扇形区域染色求出an然后说明它与an+1(n≥2)的关系式:an+an+1=3×2n(n≥2)
(3)由(2)a2+a3=3×22,a3+a4=3×23,…,an-1+an=3×2n-1,将上述n-2个等式两边分别乘以(-1)k,整理计算即可.
解答:解:(1)当n=1时,不同的染色方法种数a1=3,
当n=2时,不同的染色方法种数a2=3×2=6,
当n=3时,不同的染色方法种数a3=3×2×1=6,
当n=4时,分扇形区域1,3同色与异色两种情形
∴不同的染色方法种数a4=3×1×2×2+3×2×1×1=18
(2)证明;依次对扇形区域1,2,3,…,n,n+1染色,不同的染色方法种数为3×2n(n≥2)
其中扇形区域1与n+1不同色的有an+1种,扇形区域1与n+1同色的有an种.
∴an+an+1=3×2n(n≥2);
(3)a2+a3=3×22,a3+a4=3×23,…,an-1+an=3×2n-1,将上述n-2个等式两边分别乘以(-1)k(k=2,3,…,n-1),再相加得an=
当n=2时,不同的染色方法种数a2=3×2=6,
当n=3时,不同的染色方法种数a3=3×2×1=6,
当n=4时,分扇形区域1,3同色与异色两种情形
∴不同的染色方法种数a4=3×1×2×2+3×2×1×1=18
(2)证明;依次对扇形区域1,2,3,…,n,n+1染色,不同的染色方法种数为3×2n(n≥2)
其中扇形区域1与n+1不同色的有an+1种,扇形区域1与n+1同色的有an种.
∴an+an+1=3×2n(n≥2);
(3)a2+a3=3×22,a3+a4=3×23,…,an-1+an=3×2n-1,将上述n-2个等式两边分别乘以(-1)k(k=2,3,…,n-1),再相加得an=
|
点评:考查排列组合的应用,数列与不等式的关系的应用,数列的求和的基本方法,二项式定理的应用,考查转化思想,计算能力,难度较大

练习册系列答案
相关题目
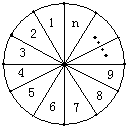 如图,将圆分成n个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为an.求
如图,将圆分成n个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为an.求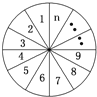 如图,将圆分成n个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为an.
如图,将圆分成n个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为an.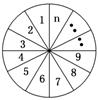
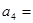 ;
;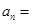 .
.