题目内容
甲、乙两名蓝球运动员分别进行一次投蓝,如果两人投进的概率分别是
、
.
(1)求两人都投进的概率;
(2)求其中恰有一人投进的概率.
| 2 |
| 3 |
| 3 |
| 5 |
(1)求两人都投进的概率;
(2)求其中恰有一人投进的概率.
分析:(1)把甲、乙二人的命中率相乘,即得两人都投进的概率.
(2)甲是否投进与乙是否投进,是相互独立的事件,把甲投进而乙没有投进的概率,加上甲没有投进而乙投进的概率,即得所求.
(2)甲是否投进与乙是否投进,是相互独立的事件,把甲投进而乙没有投进的概率,加上甲没有投进而乙投进的概率,即得所求.
解答:解:(1)设A表示“投蓝一次投进”,B表示“投蓝一次投进”,…(1分)
则“两人都投进”为A∩B,由题意可得A、B互相独立,…(4分)
∴P(A∩B)=P(A)P(B)=
×
=
….(6分)
(2)“其中恰有一人投进”表示为:(A∩
)∪(
∩B).…(9分)
P( (A∩
)∪(
∩B) )=P(A)P(
)+P(
)P(B)=
(1-
)+(1-
)×
=
.…(13分)
答:两人都投进的概率为
;其中恰有一人投进的概率
. …(14分)
则“两人都投进”为A∩B,由题意可得A、B互相独立,…(4分)
∴P(A∩B)=P(A)P(B)=
| 2 |
| 3 |
| 3 |
| 5 |
| 2 |
| 5 |
(2)“其中恰有一人投进”表示为:(A∩
. |
| B |
. |
| A |
P( (A∩
. |
| B |
. |
| A |
. |
| B |
. |
| A |
| 2 |
| 3 |
| 3 |
| 5 |
| 2 |
| 3 |
| 3 |
| 5 |
| 7 |
| 15 |
答:两人都投进的概率为
| 2 |
| 5 |
| 7 |
| 15 |
点评:本题主要考查相互独立事件的概率乘法公式,所求的事件的概率与它的对立事件的概率之间的关系,属于中档题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 、
、 .
.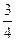 与
与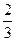 , 设甲投4球恰好投进3球的概率为
, 设甲投4球恰好投进3球的概率为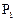 ,乙投3球恰好投进2球的概率为
,乙投3球恰好投进2球的概率为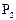 .则
.则