题目内容
 某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.(Ⅰ)甲班10名同学成绩的标准差
(Ⅱ)从两班10名同学中各抽取一人,已知有人及格,求乙班同学不及格的概率;
(Ⅲ)从甲班10人中取一人,乙班10人中取两人,三人中及格人数记为X,求X的分布列和期望.
分析:(Ⅰ)从两班成绩的茎叶图中数据的集中程度得出:甲班10名同学成绩的标准差 大于乙班10名同学成绩的标准差即可
(Ⅱ)甲班有4人及格,乙班有5人及格.事件“从两班10名同学中各抽取一人,已知有人及格”记作A,
事件“从两班10名同学中各抽取一人,乙班同学不及格”记作B,利用条件概率计算公式即可求得结论;
(III)根据题意,得到变量的可能取值,结合变量对应的事件写出变量的概率,根据变量和概率的值写出分布列,做出期望值.
(Ⅱ)甲班有4人及格,乙班有5人及格.事件“从两班10名同学中各抽取一人,已知有人及格”记作A,
事件“从两班10名同学中各抽取一人,乙班同学不及格”记作B,利用条件概率计算公式即可求得结论;
(III)根据题意,得到变量的可能取值,结合变量对应的事件写出变量的概率,根据变量和概率的值写出分布列,做出期望值.
解答:解:(Ⅰ)从两班成绩的茎叶图中数据的集中程度得出:
甲班10名同学成绩的标准差 大于乙班10名同学成绩的标准差
故答案为:>.
(Ⅱ)甲班有4人及格,乙班有5人及格.事件“从两班10名同学中各抽取一人,已知有人及格”记作A,
事件“从两班10名同学中各抽取一人,乙班同学不及格”记作B,则P(B|A)=
=
=
.(6分)
(Ⅲ)X取值为0,1,2,3P(X=0)=
•
=
;P(X=1)=
•
+
•
=
;P(X=2)=
•
+
•
=
;P(X=3)=
•
=
.(10分)
所以X的分布列为
所以E(X)=
=
.(12分)
甲班10名同学成绩的标准差 大于乙班10名同学成绩的标准差
故答案为:>.
(Ⅱ)甲班有4人及格,乙班有5人及格.事件“从两班10名同学中各抽取一人,已知有人及格”记作A,
事件“从两班10名同学中各抽取一人,乙班同学不及格”记作B,则P(B|A)=
| P(A∩B) |
| P(A) |
| ||
1-
|
| 2 |
| 7 |
(Ⅲ)X取值为0,1,2,3P(X=0)=
| ||
|
| ||
|
| 2 |
| 15 |
| ||
|
| ||||
|
| ||
|
| ||
|
| 19 |
| 45 |
| ||
|
| ||
|
| ||
|
| ||||
|
| 16 |
| 45 |
| ||
|
| ||
|
| 4 |
| 45 |
所以X的分布列为
| X | 0 | 1 | 2 | 3 | ||||||||
| P(X) |
|
|
|
|
| 19+32+12 |
| 45 |
| 7 |
| 5 |
点评:求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,只要注意解题格式就问题不大.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
(本小题满分12分)
某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图3所示,成绩不小于90分为及格.
(Ⅰ)甲班10名同学成绩标准差 乙班10名同学成绩标准差(填“>”,“<”);
(Ⅱ)从甲班4名及格同学中抽取两人,从乙班2名80分以下的同学中取一人,求三人平均分不及格的概率.
| 甲 | 乙 | |
| 257 368 24 68 | 7 8 9 10 | 89 678 1235 1 |
(本小题满分12分)
某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图5所示,成绩不小于90分为及格.
| 甲 | 乙 | |
| 257 368 58 68 | 7 8 9 10 | 89 678 1235 1 |
(Ⅰ)甲班10名同学成绩的标准差 乙班10名同学成绩的标准差(填“>”,“<”);
(Ⅱ)从两班10名同学中各抽取一人,已知有人及格,求乙班同学不及格的概率;
(Ⅲ)从甲班10人中取一人,乙班10人中取两人,三人中及格人数记为X,
|
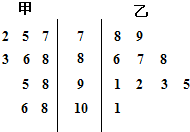 (2012•淄博一模)某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
(2012•淄博一模)某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.