题目内容
A,B两人轮流向黑板上写正整数,规则是:若a1,a2,…an出现在黑板上,则形如 | i |
分析:本题是合情推理中的难题,需要分类讨论的情况比较多,故建议模拟游戏过程,进行分析.
解答:解:∵初始状态黑板上写着5,6,而形如
aixi的数都不能写
故此时能填的数据只能从1,2,3,4,7,8,9,13,14,19中选择
如果第一个人填2,第二个人只能选3,则自己必要填1,此时先填者必输
如果第一个人填3,则第二个人还有1,2,4,7共4个数据可选,如果第二个人选2,则自己必要填1,此时先填者必输
如果第一个人填7,则第二个人还有1,2,3,4,8,9共6个数据可选,如果第二个人选4,则自己必要填1,此时先填者必输
如果第一个人填8,则第二个人还有1,2,3,4,7,9共6个数据可选,如果第二个人选4,则自己必要填1,此时先填者必输
如果第一个人填9,则第二个人还有1,2,3,4,7,8共6个数据可选,如果第二个人选7,则自己必要填1,此时先填者必输
如果第一个人填13,则第二个人还有1,2,3,4,7,8,9共7个数据可选,此时B无论选任意数,都必要填1,此时先填者必胜
故选填13者有必胜的策略.
 |
| i |
故此时能填的数据只能从1,2,3,4,7,8,9,13,14,19中选择
如果第一个人填2,第二个人只能选3,则自己必要填1,此时先填者必输
如果第一个人填3,则第二个人还有1,2,4,7共4个数据可选,如果第二个人选2,则自己必要填1,此时先填者必输
如果第一个人填7,则第二个人还有1,2,3,4,8,9共6个数据可选,如果第二个人选4,则自己必要填1,此时先填者必输
如果第一个人填8,则第二个人还有1,2,3,4,7,9共6个数据可选,如果第二个人选4,则自己必要填1,此时先填者必输
如果第一个人填9,则第二个人还有1,2,3,4,7,8共6个数据可选,如果第二个人选7,则自己必要填1,此时先填者必输
如果第一个人填13,则第二个人还有1,2,3,4,7,8,9共7个数据可选,此时B无论选任意数,都必要填1,此时先填者必胜
故选填13者有必胜的策略.
点评:穷举法是推理问题中常用的办法,根据已知条件,对每一种情况进行分析,可能得到答案.

练习册系列答案
相关题目
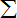
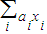 的数都不能写,不得不写1的人算输.初始状态黑板上写着5,6,问先写的人还是后写的人有必胜策略?
的数都不能写,不得不写1的人算输.初始状态黑板上写着5,6,问先写的人还是后写的人有必胜策略?