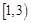题目内容
已知集合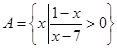 ,
,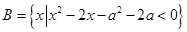
(1)当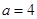 时,求
时,求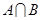 ;
;
(2)若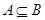 ,求实数
,求实数 的取值范围.
的取值范围.
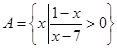 ,
,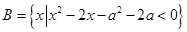
(1)当
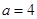 时,求
时,求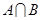 ;
;(2)若
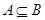 ,求实数
,求实数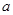 的取值范围.
的取值范围.(1) ;(2)
;(2)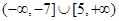 .
.
 ;(2)
;(2)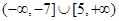 .
.试题分析:(1)集合
 分别是两不等式的解集,解两不等式就能将两集合具体化,简单化,然后利用数轴可以求出两集合的交集;(2)由(1)
分别是两不等式的解集,解两不等式就能将两集合具体化,简单化,然后利用数轴可以求出两集合的交集;(2)由(1) ,
,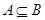 ,而集合
,而集合 是一个含有参数的一元二次不等式的解集,可对其分类讨论求解,或转化为对任意的
是一个含有参数的一元二次不等式的解集,可对其分类讨论求解,或转化为对任意的 ,都有
,都有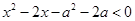 成立,从而转化为不等式恒成立问题,分离参数后可求,比分类讨论更为简单.
成立,从而转化为不等式恒成立问题,分离参数后可求,比分类讨论更为简单.试题解析:(1)
 ,
,当
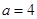 时,
时, ,
,∴
 .
. (2)
 ,
,①当
 时,
时, 
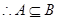 不成立;
不成立;②当
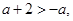 即
即 时,
时,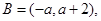
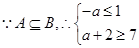 ,解得
,解得
③当
 即
即 时,
时,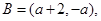
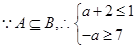 解得
解得
综上,当
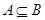 ,实数
,实数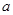 的取值范围是
的取值范围是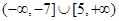 .
.
练习册系列答案
相关题目
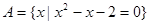 ,集合
,集合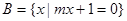 ,若
,若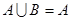 ,求实数
,求实数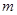 的值组成的集合.
的值组成的集合.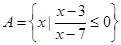 ,
,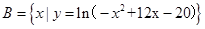 ,
,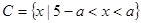
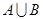 ,
,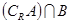 ;
;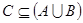 ,求a的取值范围.
,求a的取值范围.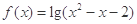 的定义域为集合
的定义域为集合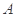 ,函数
,函数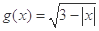 的定义域为集合
的定义域为集合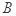 .
.
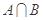 ;
;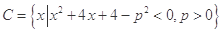 ,且
,且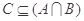 ,求实数
,求实数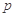 的取值范围.
的取值范围.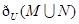 等于 ( )
等于 ( )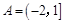 ,
,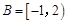 ,则
,则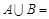 .
. 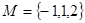 ,集合
,集合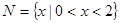 ,则
,则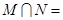 .
.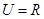 ,
,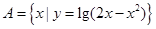 ,
,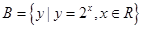 ,
,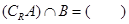
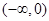
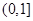
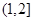
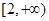
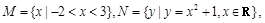 则集合
则集合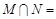 ( )
( )