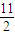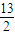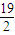题目内容
已知方程|4x-x2|-a=0有四个根，则实数a的取值范围是________．
（0，4）
分析：根据题意作出y=|4x-x2|的图象，从图象可知直线y=a与y=|4x-x2|的图象有四个交点，从而可得结论．
解答：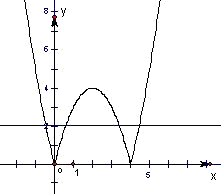
解：方程|4x-x2|-a=0?方程|4x-x2|=a．
作函数y=|4x-x2|的图象，如图．
由图象知直线y=a与y=|4x-x2|的图象应有四个交点，
当0＜a＜4时，有4个交点．
故答案为：（0，4）
点评：考查学生会根据解析式作出相应的函数图象，会根据直线与函数图象交点的个数得到方程解的个数．注意利用数形结合的数学思想解决根的存在性及根的个数判断问题．
分析：根据题意作出y=|4x-x2|的图象，从图象可知直线y=a与y=|4x-x2|的图象有四个交点，从而可得结论．
解答：
解：方程|4x-x2|-a=0?方程|4x-x2|=a．作函数y=|4x-x2|的图象，如图．
由图象知直线y=a与y=|4x-x2|的图象应有四个交点，
当0＜a＜4时，有4个交点．
故答案为：（0，4）
点评：考查学生会根据解析式作出相应的函数图象，会根据直线与函数图象交点的个数得到方程解的个数．注意利用数形结合的数学思想解决根的存在性及根的个数判断问题．
练习册系列答案
相关题目
已知方程（x2-4x-m）（x2-4x-n）=0的四个实根组成以
为首项的等差数列，则|m+n|=（ ）
| 1 |
| 2 |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
为首项的等差数列，则|m+n|=（ ）
