题目内容
不等式0≤x2+mx+5≤3恰好有一个实数解,则实数m的取值范围是________.
m=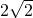
分析:由题意把问题转化为函数f(x)=x2+mx+5的最小值为3,由二次函数的最值可解.
解答:记函数f(x)=x2+mx+5,图象为开口向上的抛物线,
若函数的最小值小于3,则满足题意的x值不止一个,
故有函数的最小值为3
即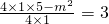 ,解得m=
,解得m=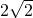
故答案为:m=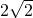
点评:本题为二次不等式解集的问题,数形结合是解决问题的关键,属基础题.
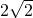
分析:由题意把问题转化为函数f(x)=x2+mx+5的最小值为3,由二次函数的最值可解.
解答:记函数f(x)=x2+mx+5,图象为开口向上的抛物线,
若函数的最小值小于3,则满足题意的x值不止一个,
故有函数的最小值为3
即
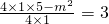 ,解得m=
,解得m=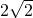
故答案为:m=
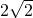
点评:本题为二次不等式解集的问题,数形结合是解决问题的关键,属基础题.

练习册系列答案
相关题目