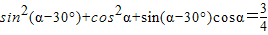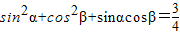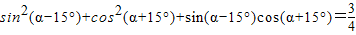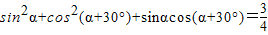题目内容
观察sin230°+cos260°+sin30°cos60°=
,sin220°+cos250°+sin20°cos50°=
和sin215°+cos245°+sin15°cos45°=
,…,由此得出的以下推广命题中,不正确的是( )
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
A、sin2(α-30°)+cos2α+sin(α-30°)cosα=
| ||
B、sin2α+cos2β+sinαcosβ=
| ||
C、sin2(α-15°)+cos2(α+15°)+sin(α-15°)cos(α+15°)=
| ||
D、sin2α+cos2(α+30°)+sinαcos(α+30°)=
|
分析:观察所给的等式,等号左边是sin230°+cos260°+sin30°cos60°=
…规律应该是sin2α+cos2(30°+α)+sinαcos(30°+α)右边的式子:
,写出结果即可进行判断.
| 3 |
| 4 |
| 3 |
| 4 |
解答:解:观察等式:
①sin230°+cos260°+sin30°cos60°=
②sin220°+cos250°+sin20°cos50°=
③sin215°+cos245°+sin15°cos45°=
,…,
照此规律,可以得到的一般结果应该是
sin2α+cos2(30°+α)+sinαcos(30°+α)右边的式子:
,
故得出的推广命题为:sin2α+cos2(30°+α)+sinαcos(30°+α)=
.
对照选项得:不正确的是(B).
故选B.
①sin230°+cos260°+sin30°cos60°=
| 3 |
| 4 |
②sin220°+cos250°+sin20°cos50°=
| 3 |
| 4 |
③sin215°+cos245°+sin15°cos45°=
| 3 |
| 4 |
照此规律,可以得到的一般结果应该是
sin2α+cos2(30°+α)+sinαcos(30°+α)右边的式子:
| 3 |
| 4 |
故得出的推广命题为:sin2α+cos2(30°+α)+sinαcos(30°+α)=
| 3 |
| 4 |
对照选项得:不正确的是(B).
故选B.
点评:本题考查类比推理,考查对于所给的式子的理解,从所给式子出发,通过观察、类比、猜想出一般规律,不需要证明结论,该题着重考查了类比的能力.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 ,sin220°+cos250°+sin20°cos50°=
,sin220°+cos250°+sin20°cos50°= 和sin215°+cos245°+sin15°cos45°=
和sin215°+cos245°+sin15°cos45°= ,…,由此得出的以下推广命题中,不正确的是( )
,…,由此得出的以下推广命题中,不正确的是( )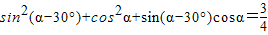
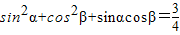
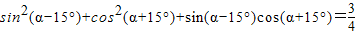
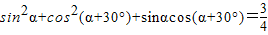
 ,sin220°+cos250°+sin20°cos50°=
,sin220°+cos250°+sin20°cos50°= 和sin215°+cos245°+sin15°cos45°=
和sin215°+cos245°+sin15°cos45°= ,…,由此得出的以下推广命题中,不正确的是( )
,…,由此得出的以下推广命题中,不正确的是( )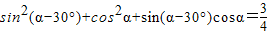
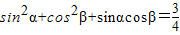
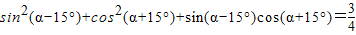
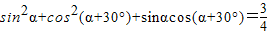
 ,sin220°+cos250°+sin20°cos50°=
,sin220°+cos250°+sin20°cos50°= 和sin215°+cos245°+sin15°cos45°=
和sin215°+cos245°+sin15°cos45°= ,…,由此得出的以下推广命题中,不正确的是( )
,…,由此得出的以下推广命题中,不正确的是( )