题目内容
命题p:“任意非零向量
,
,都有|
|+|
|>|
-
|”,则( )
| a |
| b |
| a |
| b |
| a |
| b |
分析:本题考查的知识点是,判断命题真假,并写出全称命题的否定,判断真假时可举两个向量共线反向的例子,写命题的否定时注意特称命题的格式.
解答:解:如图,
=
,
=
,
若两个非零向量
,
共线反向时,|
|+|
|>|
-
|不成立,所以命题p:“任意非零向量
,
,都有|
|+|
|>|
-
|”,是假命题;
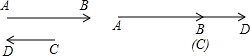
命题p:“任意非零向量
,
,都有|
|+|
|>|
-
|”,是全称命题,
其否定¬p应是特称命题,为:存在非零向量
,
,使|
|+|
|≤|
-
|.
故选B.
| AB |
| a |
| CD |
| b |
若两个非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
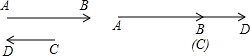
命题p:“任意非零向量
| a |
| b |
| a |
| b |
| a |
| b |
其否定¬p应是特称命题,为:存在非零向量
| a |
| b |
| a |
| b |
| a |
| b |
故选B.
点评:本题考查了命题的真假的判断与应用,考查了全称命题的否定,说明一个命题为假命题,举反例不失为一种有效的方法,全称命题的否定一定是特称命题,注意两种命题格式的书写,此题是基础题.

练习册系列答案
相关题目
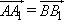 ,则四边形ABB1A1是平行四边形;
,则四边形ABB1A1是平行四边形;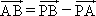 ;
;