题目内容
设函数f(x)=2sin(2x+?)+1(-π<?<0),y=f(x)的图象的一条对称轴是直线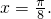
(1)求?;
(2)求函数y=f(x)的递减区间;
(3)试说明y=f(x)的图象可由y=2sin2x的图象作怎样变换得到.
解:(1)由题意知,函数图象的一条对称轴是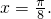 ,
,
∴ ,即
,即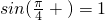
解得, ,则
,则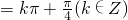
∵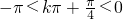 ,解得
,解得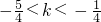 ,
,
∴k=-1,即?=- (5分)
(5分)
(2)∵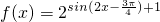 且y=2x是增函数,
且y=2x是增函数,
∴函数y=f(x)的递减区间,即为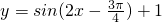 的递减区间.
的递减区间.
由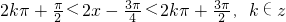 解得:
解得: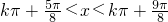 .
.
∴函数y=f(x)的递减区间为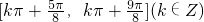 (10分)
(10分)
(3)∵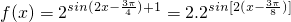
∴将函数y=2sin2x的图象向右平移 个单位,然后纵坐标扩大为2倍(横坐标不变)
个单位,然后纵坐标扩大为2倍(横坐标不变)
得到函数y=f(x)的图象(14分)
分析:(1)根据正弦曲线知,正弦函数在对称轴处的值是±1,再结合?的范围求出?的值;
(2)根据复合函数“同增异减”的法则和正弦函数的单调性,求出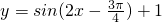 的单调区间,即为原函数的递减区间;
的单调区间,即为原函数的递减区间;
(3)根据三角函数图象的平移过程,先进行左右平移“左加右减”,要保证x的系数为1,再进行振幅变换.
点评:本题是一道综合题,考查了指数函数和正弦函数的图象以及性质,利用复合函数的法则“同增异减”求单调区间,还有利用正弦函数的图象变换得到所求函数的图象.
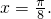 ,
,∴
 ,即
,即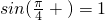
解得,
 ,则
,则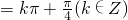
∵
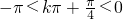 ,解得
,解得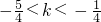 ,
,∴k=-1,即?=-
 (5分)
(5分)(2)∵
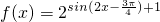 且y=2x是增函数,
且y=2x是增函数,∴函数y=f(x)的递减区间,即为
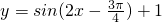 的递减区间.
的递减区间.由
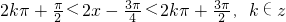 解得:
解得: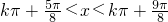 .
.∴函数y=f(x)的递减区间为
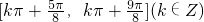 (10分)
(10分)(3)∵
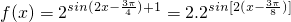
∴将函数y=2sin2x的图象向右平移
 个单位,然后纵坐标扩大为2倍(横坐标不变)
个单位,然后纵坐标扩大为2倍(横坐标不变)得到函数y=f(x)的图象(14分)
分析:(1)根据正弦曲线知,正弦函数在对称轴处的值是±1,再结合?的范围求出?的值;
(2)根据复合函数“同增异减”的法则和正弦函数的单调性,求出
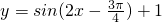 的单调区间,即为原函数的递减区间;
的单调区间,即为原函数的递减区间;(3)根据三角函数图象的平移过程,先进行左右平移“左加右减”,要保证x的系数为1,再进行振幅变换.
点评:本题是一道综合题,考查了指数函数和正弦函数的图象以及性质,利用复合函数的法则“同增异减”求单调区间,还有利用正弦函数的图象变换得到所求函数的图象.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目