题目内容
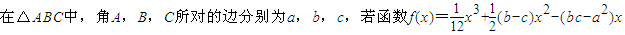 在R上为增函数,则角A的范围是( )
在R上为增函数,则角A的范围是( )A.(0,
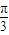 )
)B.(0,
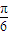 )
)C.[
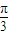 ,π)
,π)D.[
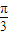 ,
,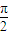 ]
]
【答案】分析:先求函数的导数,再由函数f (x)在R上单调知其导数恒为非负值,从而△≤0,从而求出cosA的取值范围,即可求得角A的范围.
解答:解: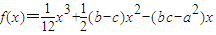 在R上为增函数
在R上为增函数
∴f'(x)= x2+(b-c)x-(bc-a2)≥0在R上恒成立
x2+(b-c)x-(bc-a2)≥0在R上恒成立
即△=(b-c)2+bc-a2=b2+c2-a2-bc≤0
cosA=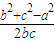 ≤
≤
∵在△ABC中∴A∈[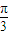 ,π)
,π)
故选C.
点评:本题主要考查函数的单调性等基本性质、导数的应用等基础知识,同时考查抽象概括能力和运算求解能力.
解答:解:
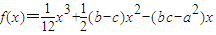 在R上为增函数
在R上为增函数∴f'(x)=
 x2+(b-c)x-(bc-a2)≥0在R上恒成立
x2+(b-c)x-(bc-a2)≥0在R上恒成立即△=(b-c)2+bc-a2=b2+c2-a2-bc≤0
cosA=
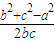 ≤
≤
∵在△ABC中∴A∈[
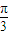 ,π)
,π)故选C.
点评:本题主要考查函数的单调性等基本性质、导数的应用等基础知识,同时考查抽象概括能力和运算求解能力.

练习册系列答案
相关题目
在△ABC中,角A,B,C所对的边分别为a,b,c,若函数f(x)=
x3+
(b-c)x2-(bc-a2)x在R上为增函数,则角A的范围是( )
| 1 |
| 12 |
| 1 |
| 2 |
A、(0,
| ||||
B、(0,
| ||||
C、[
| ||||
D、[
|
 在R上为增函数,则角A的范围是
在R上为增函数,则角A的范围是 )
) )
) ]
]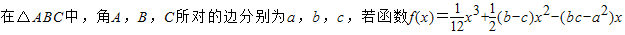 在R上为增函数,则角A的范围是( )
在R上为增函数,则角A的范围是( )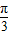 )
)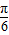 )
)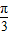 ,π)
,π)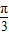 ,
,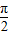 ]
]