题目内容

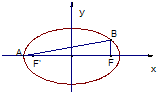
过椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左顶点A且斜率为k的直线交椭圆C于另一点B，且点B在x轴上的射影恰为右焦点F，若k=
1
2
，则椭圆的离心率e的值为
 
．
分析：由于点B在x轴上的射影恰为右焦点F，可得B(c，
b2
a
)．又A（-a，0），利用向量计算公式可得
1
2
=k=
b2
a
-0
c+a
，化简并利用离心率计算公式即可得出．
解答：解：∵点B在x轴上的射影恰为右焦点F，∴B(c，
b2
a
)，
又A（-a，0），
∴
1
2
=k=
b2
a
-0
c+a
，化为ac+a2=2b2=2（a2-c2），
化为2c2+ac-a2=0，
∴2e2+e-1=0，解得e=
1
2
．
故答案为：
1
2
．
点评：本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题，属于基础题．
练习册系列答案
相关题目
过椭圆C：
x2
a
2
 
+
y2
b
2
 
=1(a＞b＞0)的一个顶点作圆x2+y2=b2的两条切线，切点分别为A，B，若∠AOB=90°（O是坐标原点），则椭圆C的离心率为
 
．
精英家教网过椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左顶点A的斜率为k的直线交椭圆C于另一个点B，且点B在x轴上的射影恰好为右焦点F，若
1
3
＜k＜
1
2
，则椭圆离心率的取值范围是
 
．
（2003•朝阳区一模）已知：如图，过椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左焦点F（-c，0）作垂直于长轴A1A2的直线与椭圆c交于P、Q两点，l为左准线．
（Ⅰ）求证：直线PA2、A1Q、l共点；
（Ⅱ）若过椭圆c左焦点F（-c，0）的直线斜率为k，与椭圆c交于P、Q两点，直线PA2、A1Q、l是否共点，若共点请证明，若不共点请说明理由．
（2010•龙岩二模）过椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的一个焦点F且垂直于x轴的直线交椭圆于点(-1，
2
2
)．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在过点A（-2，0）的直线l与椭圆C交于两点M、N，使得|FP|=
1
2
|MN|（其中P为弦MN的中点）？若存在，求出直线l的方程；若不存在，请说明理由．
精英家教网如图，已知直线L：x=my+1过椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点F，且交椭圆C于A、B两点，点A、B在直线G：x=a2上的射影依次为点D、E．
（1）若抛物线x2=4
3
y的焦点为椭圆C的上顶点，求椭圆C的方程；
（2）若N(
a2+1
2
，0)为x轴上一点，求证：
AN
=λ
NE
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网